Capacité thermique du propylène glycol ; chaîne de mesure de la température : BTS AVA 2010.

Mesure de la capacité thermique du propylène glycol. Pour mesurer les quantités de chaleur mises en jeu au cours de transformations quelconques, on utlilise un calorimètre, enceinte quasi-adiabatique. les expériences sont réalisées sous pression constante ( pression atmosphérique ). Q, la quantité d'énergie thermique reçue par le système, est égale à sa variation d'enthalpie DH. Etalonnage du calorimètre. Avant toute mesure, il est indispensable de connaître la capacité thermique du calorimètre et de ses accessoires. On mesure cette capacité thermique C dans des conditions aussi proches que possible de l'expérience. Un conducteur métallique de résistance R = 40 ohms est immergé dans une masse m = 200 g d'eau dont la capacité thermique massique c =4180 J K-1 kg-1. L'ensemble est placé dans un calorimètre de capacité thermique C. Le conducteur est soumis à une tension U et parcouru par le courant d'intensité I = 0,75 A pendant l'intervalle de temps Dt = 8 min. Il cède une quantité d'énergie notée Q1. Ecrire la relation liant Q1, U, I et Dt. En déduire la relation liant Q1, R, I et Dt. Q1= U  I   Dt ; U = RI, d'où Q1= R  I2  Dt. Lorsque la température du calorimètre et de son contenu augmente de Dq = 12°C, l'ensemble reçoit une quantité d'énergie thermique notée Q2. Ecrire la relation liant Q2, C, m, c et Dq. Q2 =  (C+ m c ) Dq. Ecrire la relation liant Q1 et Q2 en justifiant. Le calorimètre est quasi-adiabatique : les échanges entre le calorimètre et l'extérieur sont quasi-nuls. Q1 = Q2.   Montrer que la capacité thermique du calorimètre s'exprime par : C =RI2Dt / Dq -mc . Q1 = Q2. R  I2  Dt = (C+ m c ) Dq ;   R  I2  Dt / Dq = C + mc ;  C =RI2Dt / Dq -mc . Calculer C en précisant son unité. C = 40 *0,752 *8*60 / 12 -0,200*4180 =900-836= 64 J K-1. Mesure de capacité thermique. On remplace la masse d'eau par la même masse de propylène glycol ( PG) pur, de capacité thermique cPG et à la même température  ambiante qA =22°C. On déclenche le chauffage au temps t= 40 s et on le laisse fonctionner pendant 8 min. Le conducteur est soumis à la même tension et parcouru par le même  courant que lors de l'étalonnage du calorimètre. On enregistre la température q en fonction du temps t. Calculer la variation de température subie par le propylène glycol pendant la chauffe. 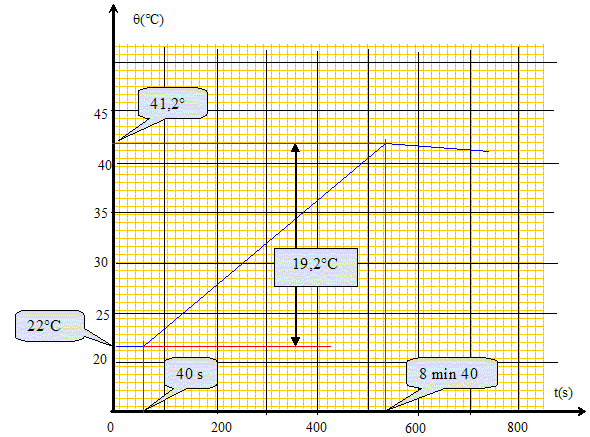La courbe comporte trois parties distinctes. Justifier l'allure de la courbe à partir de t = 520 °C. Le calorimètre est un système quasi-adiabatique : les échanges d'énergie avec l'extérieur ne sont pas nuls. La température du calorimètre décroît lentement dès que le système de chauffage est arrèté. Par analogie avec la relation ci-dessus, donner l'expression de cPG. Q1 = Q2. R  I2  Dt = (C+ mcPG ) Dq ;   R  I2  Dt / Dq = C + mcPG ;  cPG = ( R  I2  Dt / Dq - C ) / m. A.N : cPG =(40*0,752*8*60 / 19,2 -64) /0,200 =2492,5 ~2,49 kJ kg-1 K-1. Le rôle d'un liquide de refroidissement est d'évacuer les calories d'un système qui en produit plus qu'il ne peut en évacuer naturellement. Pourquoi est-il intéressant que la capacité thermique d'un liquide de refroidissement soit très élévée ? La quantité d'énergie à évacuer par le liquide est proportionnelle à la capacité thermique massique du liquide de refroidissement. La chaine de mesure de température. L'évolution de la température dans le calorimètre est suivie grâce à un ordinateur par l'intermédiaire  de la chaîne suivante :  La tension délivrée par le capteur de température doit être amplifiée afin de travailler sur une plage de 0 à 5 V. Etude du capteur de température. La mesure de température dans le calorimètre précédent est réalisée à l'aide d'un capteur de température à sortie analogique, qui est utilisable dans le domaine des température comprises entre 0°C et 100 °C. L'étalonnage du capteur est effectué en relevant l'évolution de sa tension de sortie UC, en fonction de la température du calorimètre, notée q. q(°C) 0 20 40 60 80 100 UC ( mV) 0 200 390 580 780 980 Tracer la courbe UC = f(q) et vérifier que UC =9,8 q avec UC en mV et q en °C , sur la plage [0 ; 100°C ]. 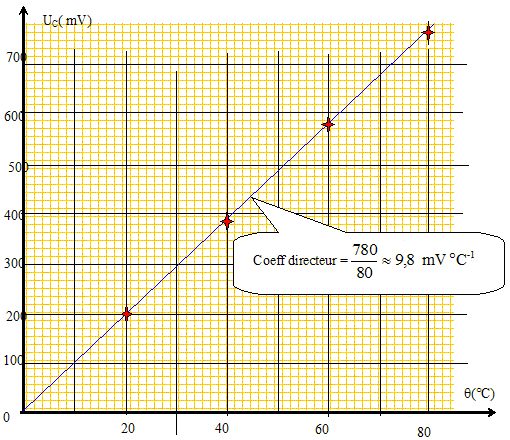Calculer la sensibilité du capteur s = Dy/Dx. On précisera son unité. Dériver l'expression précédente par rapport à q. s = dUC / dq = 9,8 mV °C-1. Quelle est la variation de la tension DUC que l'on mesure à la sortie du capteur lorsque sa température varie de 0,5 °C ? DUC = 9,8 *0,5 = 4,9 mV. Pour cette référence, le constructeur donne une sensibilité caractéristique de 10 mV / °C + ou - 0,2 mV /°C. La sensibilité du modèle étudié est-elle conforme à la valeur caractéristique qu'indique le constructeur ? La sensibilité indiquée par le constructeur est comprise entre 9,8 mV/°c et 10,2 mV/°C. Nous avons trouvé 9,8 mV /°C. La sensibilité du modèle est donc conforme. Amplification de la tension délivrée par le capteur. On souhaite mesurer des températures entre 0°C et 100°C. Pour cela, il faut que cet écart de température corresponde à un écart de 5 V à l'entrée de la carte d'acquisition. US comprise entre 0 et 5 V. C'est pourquoi on amplifie la tension de sortie du capteur de manière à obtenir la relation :  US = 5,1 UC. US : tension de sortie de l'adaptateur ( en V) ; UC : tension de sortie du capteur de température ( en V). Montrer que la température du capteur est alors reliée à la tension de sortie US par la relation : q = 20 US avec q en °C et US en V. D'une part US = 5,1 UC ; d'autre part UC = 9,8 10-3 q. US = 5,1*9,8 10-3 q ; US = 5,1*9,8 10-3 q = 0,05 q  ;  q = US /0,05 = 20 US. La carte d'acquisition permet l'observation d'une variation minimale de tension de 20 mV. Calculer la variation minimale Dqmin de température correspondante. Dqmin = 20 *0,020 = 0,4 °C. Etude du convertisseur analogique numérique ( CAN). Le CAN traduit le signal analogique US en grandeur numérique. A chaque instant, il affiche un nombre de sortie NS codé sur n bits. Ce nombre est égal à la partie entière du rapport  US / q avec US : tension d'entrée du CAN ( en volt) et q : quantum ou résolution du CAN ( en volt ). Le quantum correspond au pas de conversion du CAN et il est calculable par la relation : q =( USmax-USmin) / 2n. Avec n : nombre de bits ; USmax : tension maximale d'entrée du CAN ; USmin : tension minimale d'entrée du CAN. On considère un CAN dont le quantum q = 100 mV.   Calculer le nombre NS qu'il affiche lorsque la tension d'entrée US vaut 1,2 V puis donner la valeur binaire de ce nombre codé sur 4 bits. NS = US / q = 1,2 / 0,100 = 12. 12 = 1*23 +1*22 +0*21+0*20. Ce nombre s'écrit en binaire : 1100. On dispose de 2 CAN ( à 4 bits et à 8 bits ) ayant une plage d'utilisation en tension allant de 0 à 5 V. On appelle q4 et q8 respectivement les quantums des CAN à 4 bits et à 8 bits. Calculer en mV les quantums q4 et q8. q4 =(5-0) / 24 =0,3125 V ~ 313 mV.   q8 =(5-0) / 28 =0,0195 V ~ 20 mV. Compte tenu de la précision 20 mV voulue dans la lecture de US, quel CAN doit-on utiliser ? Le CAN 4 bits n'est pas assez précis ; on choisit le CAN 8 bits. En supposant que le CAN choisit est à 8 bits, calculer le nombre possible de valeurs numériques qu'il peut fournir en sortie. 28 = 256.

menu