On
souhaite vérifier la concentration massique en ion sulfate dans une eau
minérale, sachant que l'étiquette de la bouteille indique C= 1,2 g/L. A
cette fin on effectue un dosage de l'eau étudiée par une solution
aqueuse de chlorure de baryum ( Ba2+ ; 2 Cl- ). On utilise la propriété de très faible solubilité du sulfate de baryum BaSO4
dans l'eau. Lorsqu'une solution titrante contenant des ions baryum est
ajoutée à l'eau minérale à doser contenant des ions sulfates, un
précipité de BaSO4 se forme. On peut suivre le dosage par conductimétrie.
Etude de l'ion sulfate.
16S : 1s2 2s2 2p6 3s2 3p4. 8O : 1s2 2s2 2p4.
L'oxygène se trouve dans la deuxième période et dans la seixième colonne de la classification périodique des éléments.
En déduire l'emplacement du soufre dans cette classification.
Le niveau n=3 est en partie occupé : donc 3ème période.
La structure électronique externe de l'oxygène et du soufre sont identiques ( 2s2 2p4 et 3s2 3p4) : donc le soufre appartient à la même colonne que l'oxygène.
On donne la structure de Lewis de l'ion sulfate :
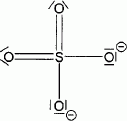
|
En appliquant les règles du modèle VSEPR à l'ion sulfate, donner la géométrie autour de l'atome de soufre. Argumenter la réponse.
Dans cette méthode, une liaison multiple est équivalente à une liaison simple.
Le soufre est lié à 4 autres atomes ( 4 directions de liaison).
Le soufre ne possède aucun doublet non liant.
Donc type AX4, tétraèdrique.
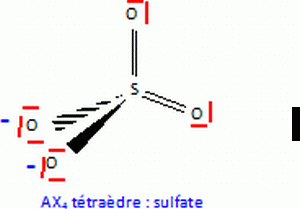
|
Dosage conductimétrique des ions sulfate dans une eau minérale.
On négligera la très faible dissolution du solide BaSO4 dans l'eau.
On place dans un becher un volume V = 50 mL d'eau minérale à doser,
ainsi que 200 mL d'eau distillée. On dose les ions sulfate présents
dans cette eau par une solution aqueuse de chlorure de baryum telle que
[Ba2+]=c0=5,5 10-2 mol/L.
On relève la conductivité s de la solution en fonction du volume de solution de chlorure de baryum ajouté. On donne la courbe de dosage.
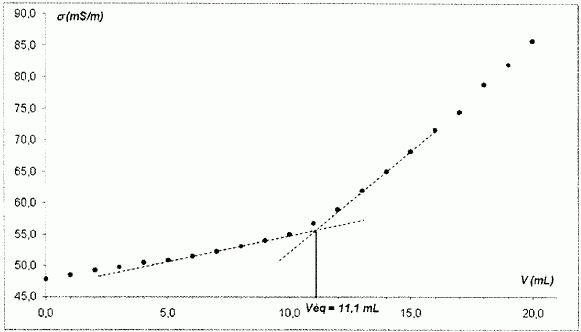
Si on avait choisi un bécher de 100 mL pour doser directement le volume V d'eau minérale, la cellule conductimétrique aurait-elle été parfaitement immergée ?
On mesure la conductivité d'une portion de liquide située dans la
lucarne ( de longueur voisine de 5 cm) située à l'extrémité de la
sonde du conductimètre. Avec un becher de 100 mL et 50 mL d'eau
minérale, la cellule de mesure n'aurait pa été correctement immergée.
Pourquoi a t-on préféré un becher de 500 mL et l'ajout d'eau distillée
?
La cellule de mesure est correctement immergée.
Le
volume total du liquide contenu dans le becher varie peu au cours
du dosage ( de 250 à 270 mL soit une variation de 10%). Le volume
de la solution contenue dans le becher peu être considéré comme
constant.
Le technicien doute de l'exactitude de la concentration de la solution de chlorure de potassium ( K+ ; Cl- ) utilisée pour étalonner le conductimètre.
Le résultat du dosage risque t-il d'être faussé ?
Non. On n'a pas besoin de la valeur de la conductivité de la solution ;
il nous suffit de repérer l'intersection de deux droites pour
déterminer l'équivalence du dosage.
Ecrire
l'équation de la réation mise en jeu lors du dosage et calculer sa
constante d'équilibre ( notée K). Que peut-on en conclure ?
On donne Ks = [Ba2+ aq] [SO42- aq] =1,0 10-10.
Ba2+ aq + SO42- aq = BaSO4(s).
K = 1 / ( [Ba2+ aq] [SO42- aq]) = 1/Ks = 1,0 1010.
K est très grand : la réaction est totale.
|
Etablir l'expression littérale de la concentration [SO42- aq] en ion sulfate dans l'eau minérale en fonction de V, c0 et Véq.
Quantité de matière en ion sulfate dans V mL d'eau minérale : V [SO42- aq] ( en mmol )
Quantité de matière d'ion baryum versé à l'équivalence : c0Véq ( en mmol ).
A l'équivalence les quantités de matière des réactifs sont en proportions stoechiométriques.
V [SO42- aq] = c0Véq ; [SO42- aq] = c0Véq / V.
Calculer la valeur de la concentration en ion sulfate.
[SO42- aq] =5,5 10-2 *11,1 / 50 = 0,0121 ~0,012 mol/L.
Le résultat est-il compatible avec la concentration indiquée sur la bouteille d'eau minérale c= 1,2 g/L ?
On donne M(SO42-) = 96,1 g/mol.
Cexp =0,0121 M(SO42-) =0,0121*96,1 =1,16 ~1,2 g/L.
Ecart relatif (1,2-1,16)*100 / 1,2 ~ 3 %.
A 3 % près les deux valeurs sont compatibles.
|
|
|
|


