La lumière, une onde électromagnétique : bac S Amérique du Nord 2010

L'onde lumineuse et ses caractéristiques. On rappelle que dans le vide, toutes les ondes électromagnétiques ont la même célérité c = 3,00 108 m/s. Pour une radiation de fréquence n, dont la période est T et de longueur d'onde l, se propageant dans le vide à la célérité c, on propose les relations suivantes : (a) : l = c/n ; (b) : T = c/ l ; (c) : l = cT. Donner la définition de la longueur d'onde . La longueur d'onde ( mètre) est la distance parcourue par le front de l'onde se déplaçant à la célérité c ( m/s), en une période T(s). Préciser l'unité de l et choisir dans les relations précédentes la (les) relation(s) correcte(s). La longueur d'onde s'exprime en mètre, la célérité en m/s, la période T en seconde et la fréquence en hertz ou s-1.  [c / n] = L T-1 / T-1 = L T-1 T  = L ; (a) convient. [c / l] = L T-1 L-1  = T-1  ; (b) n'est pas homogène, elle ne convient pas. [cT] = L T-1 T = L ; (c) est homogène, elle convient. Une lampe à vapeur de lithium émet dans le vide une radiation intense de longueur d'onde l = 571 nm.. Déterminer la fréquence de cette radiation. n = c/l = 3,00 108 / 571 10-9 =5,25 1014 Hz.   La radiation émise par la lampe à vapeur de lithium traverse un milieu transparent d'indice n = 1,5. Un élève curieux s'interroge sur les caractéristiques de cette radiation dans ce milieu transparent puis il affirme "la fréquence est inchangée et la longueur d'onde est mainteant 380 nm". Ces affirmations sont-elles justes ou érronées ? Justifier. La fréquence caractérise une onde ; elle est constante quel que soit le milieu. La longueur d'onde, comme la célérité dépendent du milieu de propagation. n = c / v avec v : célérité de la lumière dans le milieu transparent. lmilieu = v / n = c / (nn) = lvide / n = 571/1,5 =381 nm. Les affirmations de l'élève sont correctes. Analyse d'une lumière complexe ; le spectrophotomètre à prisme. Ce spectrophotomètre utilise les propriétés dispesives d'un prisme en verre. Lorsqu'une lumière polychromatique est dirigée vers une face du prisme, chaque radiation est déviée d'un angle qui dépend de l'indice et donc de la longueur d'onde dans le vide l. Ci-dessous est représenté la variation de l'indice d'un verre en fonction de la longueur d'onde l. 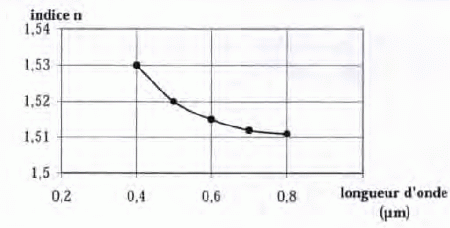Qu'appelle t(on lumière polychromatique ? "polychromatique" : plusieurs couleurs. Une lumière polychromatique est composés de plusieurs radiations de fréquences différentes. A quelles couleurs sont associées les longueurs d'onde correspondant aux limites du visible ? 400 nm est associé au violet ; 800 nm est associé au rouge. Déterminer les indices du prisme en verre pour ces longueur d'ondes limites. 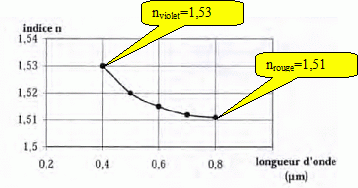Une lumière émise par une lampe à vapeur de mercure contient trois radiations intenses de longueur d'onde : 440 nm, 550 nm et 580 nm. On place sur le trajet de la lumière un filtre qui ne laisse passer que la radiation de longueur d'onde 440 nm et on l'envoie verre le prisme réalisé avec le verre précédent sous une incidence i1 = 45°. le rayon subit une première réfraction en I sur la face AB d'entrée du prisme. On rappelle la loi de la réfraction : n1 sin i1 = n2 sin i2. Milieu (1) : air d'indice n1 = 1 quel que soit l ; milieu (2) : le verre. 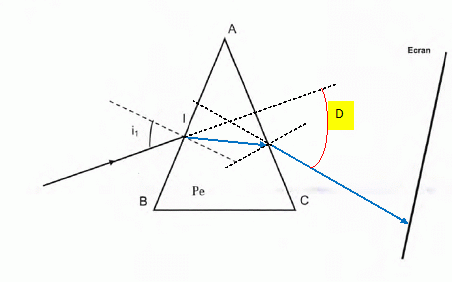Déterminer l'angle de réfraction dans le prisme pour cette radiation. Tracer le rayon réfracté à l'intérieur du prisme. sin i2 =n1 sin i1 / n2  = 1*sin45 / 1,53 =0,462 ; i2 = 27,52 ~28°. On enlève le prisme et un écran est placé après le prisme.  Que visualise t-on sur l'écran lorsque le prisme reçoit l'ensemble de la lumière émise par la lampe à vapeur de mercure ? Justifier. 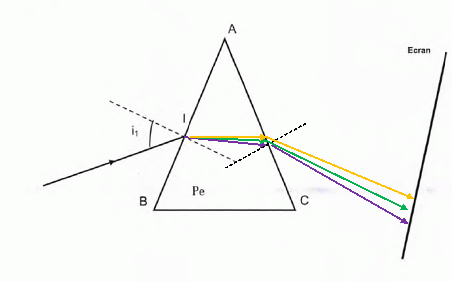L'indice du prisme diminue lorsque la longueur d'onde augmente ; en conséquence l'angle de réfraction va croître et l'angle de déviation  va diminuer. Emission de la lumière. La radiation la plus intense émise par la lampe à vapeur de mercue est de couleur violette et correspond à l= 440 nm. Exprimer le quantum d''énergie associé à cette émission. E = h c / l. A.N : E = 6,63 10-34 *3,00 108 / 440 10-9 =4,52 10-19 J. 4,52 10-19 /1,60 10-19 =2,83 eV. Comment interprète t-on l'émission de photons par les atomes ? L'énergie de l'atome est quantifiée. Lors du retour d'un atome "excité"  dans un état de moindre énergie, celui-ci cède au milieu extérieur son surplus d'énergie sous forme d'un photon.

menu