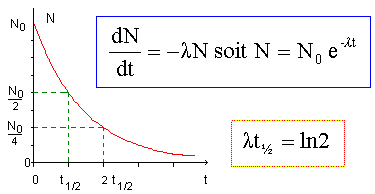Principe de
l'électrolyse d'une solution de chlorure de sodium :
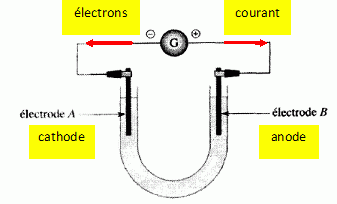
Un tube eb U muni de deux électrodes joue le rôle d'électrolyseur. Il
contient une solution de chlorure de sodium( Na+aq +Cl-aq).
Les deux électrodes A et B sont reliées chacune aux bornes positive et
négative d'un générateur de tension continue.
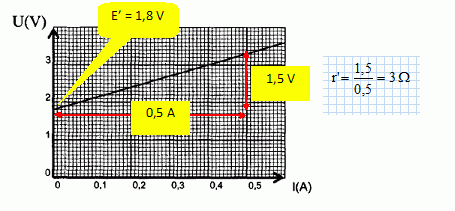
L'étude expérimentale permet d'obtenir la courbe caractéristique
modélisée de l'électrolyseur donnant l'évolution de U aux bornes de
l'électrolyseur en fonction de l'intensité I du courant qui le traverse.
L'électrolyseur est caractérisé par sa force contre électromotrice E'
et sa résistance interne r'.
Donner l'expression
générale de la tension U aux bornes d'un électrolyseur.
U = E' + r'I.
Déterminer
graphiquement E' et r'.
E' : ordonnée à l'origine ; r' : coefficient directeur de la droite.
|
Après plusieurs minutes de
fonctionnement, on identifie les produits formés :
- à une électrode, il s'est formé des ions hypochlorite :
Cl-aq + 2HO-aq = ClO-aq + H2O(l)
+ 2e-.
- à l'autre électrode, il se forme du dihydrogène gazeux et des ions
hydroxyde HO- :
2H2O(l)
+ 2e- = H2(g) + 2HO-aq sodium.
|
Compléter
le schéma de l'électrolyseur en indiquant l'anode, la cathode, le sens
de déplacement des électrons dans les fils.
Voir schéma ci-dessus.
Identifier
l'électrode où se forme les ions hypochlorite.
Cl-aq
+ 2HO-aq = ClO-aq + H2O(l) + 2e-.
(1)
Les ions chlorures s'oxydent et libèrent des électrons ; une oxydation
se produit à l'anode positive de l'électrolyseur.
Etude
d'un électrolyseur de piscine.
L'électrolyse est réalisée par un coffret
d'alimentation électrique délivrant une tension continue U = 10,0 V.
L'intensité du courant, considérée comme constante vaut I = 20,0 A.
Montrer
que la charge électrique circulant dans le dispositif pendant la durée Dt = 30,0 min a pour valeur Q =
3,60 104 C.
Q = IDt = 20,0 * 30*60 =3,6 104
C.
Exprimer
puis calculer la quantité de matière d'ion hypochlorite notée n(ClO-)
que peut produire cette électrolyse en 30,0 min de fonctionnement.
On donne 1 F = 9,65
104 C mol-1.
Quantité de matière d'électrons : n(e-) = Q / F = 3,6 104 / 9,65 104
=0,373 mol.
Quantité de matière d'ion hypochlorite : les nombres stoechiométriques
de la demi-équation (1) conduisent à :
n(ClO-) = ½n(e-) = ½ IDt /
/ F =
0,187 mol.
Irridium 192 et curithérapie.
Pour détruire certaines tumeurs, on utilise l'irridium 19277Ir à partir duquel on obtient, par désintégration, un noyau de platine 19278Pt, une particule chargée, ainsi qu'un rayonnement g. La période ou demi-vie de l'irridium est T = 74 jours.
Ecrire l'équation de désintégration de l'irridium 192 en indiquant les lois utilisées.
19277Ir ---> 19278Pt* + 0-1e suivi de : 19278Pt* ---> 19278Pt +00g.
Conservation de la charge : 77 = 78-1 ; conservation du nombre de nucléons : 192 = 192 +0.
Donner le nom de la particule émise et le type de radioactivité.
La particule émise est un électron ; le type de radioactivité est ß-.
l'expression
générale de l'évolution temporelle du nombre N(t) de noyaux radioactifs
d'un radioélément en fonction du temps est : N(t) = N0 exp(-l t).
l étant la constante radioactive et N0 le nombre de noyaux radioactifs initiaux dans l'échantillon étudié.
|
Donner la définition de la période radioactive.
La période ou demi-vie radioactive, notée T ou t½, est la durée au bout de laquelle l'activité initiale est divisée par 2.
Etablir la relation l = ln2 / T puis calculer l en jour-1.
N(T) = ½N0 = N0 exp(-l T).
0,5 = exp(-l T) ; ln 0,5 = -ln 2 = -l T ; l = ln2 /T = ln2 / 74 = 9,367 10-3 ~9,4 10-3 jour-1.
Tracer sur la copie l'allure de la courbe de décroissance radioactive N= f(t) en précisant en fonction de N0 les ordonnées des points d'abscisses t=0, t =T et t = 2T..
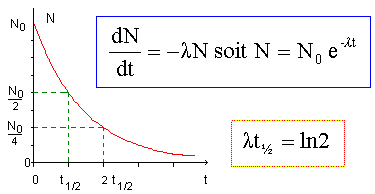
On
suppose que le corps humain ne contient pas d'irridium 192
initialement. A la date t=0, on implante à un patient un fil de platine
irridié ( alliage de platine et de 20 % d'irridium ) contenant N0 = 8,0 104 noyaux d'irridium 192.
Déterminer le nombre de noyaux d'irridium 192 restants dans le patient aux instants de dates t1 = 74 jours, t2 = 148 jours et t3 = 222 jours.
A t = t1 = T, il reste ½N0 = 4,0 104 noyaux d'irridium 192.
A t = t2 = 2T= 148 jours, il reste 0,25N0 = 2,0 104 noyaux d'irridium 192.
A t = t3 = 3T= 222 jours, il reste 0,125N0 = 1,0 104 noyaux d'irridium 192.
On considère qu'au bout de deux ans, la quantité de noyaux restants est négligeable par rapport à celle introduite.
Vérifier numériquement cette information.
2 ans = 2*365 = 730 jours.
N(2ans) = 8,0 104 exp(- 9,367 10-3* 730) = 86.
ou N(2ans) / N0 = 1,1 10-3.
|
|