Le
dispositif étudié doit asservir la position angulaire des pales à la
valeur numérique Nc délivrée par le micro-contrôleur. En
fonction de la vitesse du vent, le dispositif reçoit une consigne
angulaire d’inclinaison des pales, sous la forme d’une information
numérique Nc, codée sur 4 bits. Un moteur à courant continu
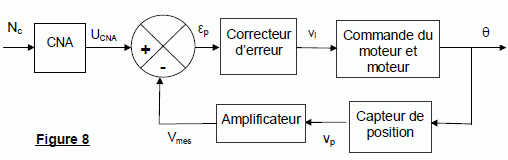
oriente les pales dans la position attendue q. Une vue d’ensemble de
l’asservissement est
donnée figure 8.
Conversion
Numérique-Analogique.
Cette fonction est réalisée par le circuit schématisé sur la figure 9.
La consigne angulaire Nc codée sur 4 bits (a3, a2,
a1, a0) est convertie en une tension analogique UCNA.
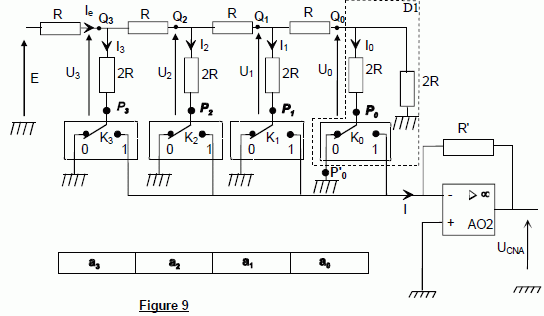
Pour i = 0, 1, 2 ou 3, la position de
l'interrupteur Ki dépend de la valeur du bit ai :
Si ai = 0 alors Ki est en position 0 et si ai
= 1 alors Ki est en position 1.
|
Quel est le régime
de fonctionnement de l'amplificateur opérationnel AO2 ?
La présence d'une boucle de contre réaction entre l'entrée inverseuse
et la sortie indique que l'AO2 peut fonctionner en régime
linéaire.
En
déduire que les tensions entre les points P0, P1, P2 ou P3 et la masse du
montage peuvent être considérées comme nulles quelles que soient les
positions des interrupteurs Ki.
Lorsque les interrupteurs Ki sont en position 0,
les points P0, P1, P2 ou P3
sont reliés à la masse.
Lorsque les
interrupteurs Ki sont en position 1,
les points P0, P1, P2 ou P3
sont reliés à l'entrée inverseuse de l'AO2.
En régime linéaire, les deux entrées de l'AO2 sont au même
potentiel, celui de la masse dans ce cas.
Les
tensions entre les points
P0, P1, P2 ou P3 et la
masse peuvent être considérées comme nulles quelles que soient
les positions des interrupteurs Ki.
|
Exprimer la tension UCNA
en fonction de l'intensité I.
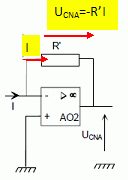
Justifier
que l'intensité I puisse s'écrire: I
= a3.I3 + a2.I2 + a1.I1
+ a0.I0.
Les intensités I0, I1, I2, I3
s'ajoutent ( loi des noeuds) lorsque les ai valent 1. Par
contre si ai = 0, l'intensité Ii n'apporte pas sa
contribution à I. ( interrupteur Ki ouvert )
Déterminer
la résistance équivalente Re au dipôle passif D1
situé à droite des bornes Q0 et P'0 et en déduire
l'expression de U0 en fonction de U1.
Deux résistances de même valeur 2R montées en dérivation ; Re
= ½(2R) = R.
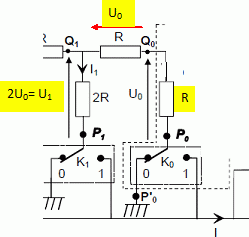 U0 = ½U1. U0 = ½U1.
Appliquer le même
raisonnement pour exprimer U1 en fonction de U2 puis
U2 en fonction de U3 et enfin U3 en
fonction de E.
U1 = ½U2
; U2 = ½U3
; U3 = ½E.
Montrer
que l'intensité I3 peut s'écrire
: I3 = E /
(4R). En déduire
l’expression de I2, I1 et I0.
U3 =2 R I3
et U3 = ½E,
par suite I3 = E /
(4R).
I2=U2
/(2R) ; U2 = ½U3
et U3 = ½E ;
d'où U2 =0,25
E, par suite I2=0,25 E /(2R) = E/(8R).
I1=U1
/(2R) ; U1 = ½U2
et U2 =0,25 E ; d'où U1 =0,125
E, par suite I1=0,125 E /(2R) = E/(16R).
I0=U0
/(2R) ; U0 = ½U1
et U1 =0,125
E ; d'où U0 = E /
16, par suite I0= E/(32R).
En remplaçant les
intensités des courants par les expressions déterminées ci-dessus,
exprimer UCNA en fonction de E,
R, R' et les valeurs des bits a0, a1, a2 et a3.
I = a3.I3 + a2.I2
+ a1.I1 + a0.I0 = E/R [a3/4+ a2./
8 + a1 / 16 + a0./ 32 ]
UCNA=-R'I
= -R'E / R [a3/4+ a2/
8 + a1 / 16 + a0/ 32 ].
UCNA=-R'I
= -R'E / (32R) [23a3+
22a2 + 2 a1+ a0 ].
En déduire que l'on
peut écrire UCNA = q.NC. Préciser
l'expression de q.
On pose NC
=23a3+ 22a2
+ 2 a1+ a0 ; q = -R'E / (32R) ; d'où UCNA = qNC.
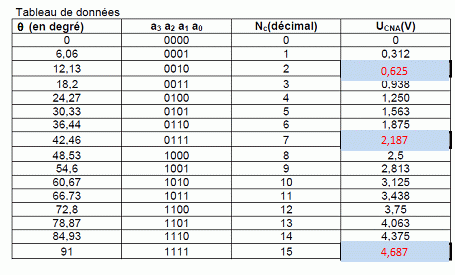
Compléter les 3
cases vides du tableau. On donne E = - 10 V et R = R' = 27 kW.
|
En déduire la valeur
numérique du quantum q.
q
= -R'E / (32R) =
10/32= 0,3125~ 0,312 V.
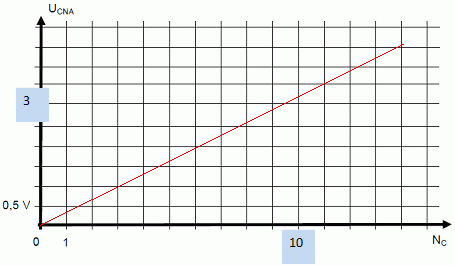
Tracer la
caractéristique de transfert du CNA.
|
|



 U0 = ½U1.
U0 = ½U1.
