Etude du hacheur.
On suppose que le moteur à courant continu est commandé par un hacheur
série.
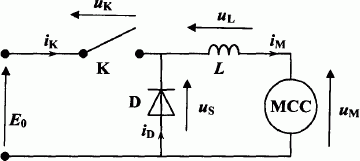
On
a placé une bobine de forte inductance L avec le moteur. La source
continue en entrée du hacheur délivre une tension de valeur E0
= 800 V.
l'interrupteur K est commandé périodiquement de la façon suivante sur
une période T :
- il est fermé pour t compris entre 0 et t1 = aT,
- il est ouvert pour t compris entre t1 et t2 = T.
a est appelé rapport cyclique de hachage.
On supposera que la diode D et l'interrupteur K sont idéaux.
Quel
composant électronique de puissance peut-on choisir pour K ?
Transistor ou bien thyristor.
|
Le hacheur fonctionne en
conduction ininterrompue ( le courant iM(t) est peu ondulé
et ne s'annule jamais ).
Quel
est le rôle de la diode D dite " diode de roue libre" ?
Lorsque
l'interrupteur K conduit, la bobine inductive stocke de l'énergie.
Lorsque l'interrupteur K est ouvert, la bobine restitue l'énergie
qu'elle a stockée, la diode D étant passante, elle ferme le
circuit moteur + bobine d'inductance L. En conséquence, le courant iM(t)
est peu ondulé et ne s'annule jamais.
|
On a relevé les
oscillogrammes de l'intensité iM(t) dans la charge et la
tension de sortie du hacheur uS(t).
Compléter les formes
d'ondes des signaux uK(t), iK(t) et iD(t).
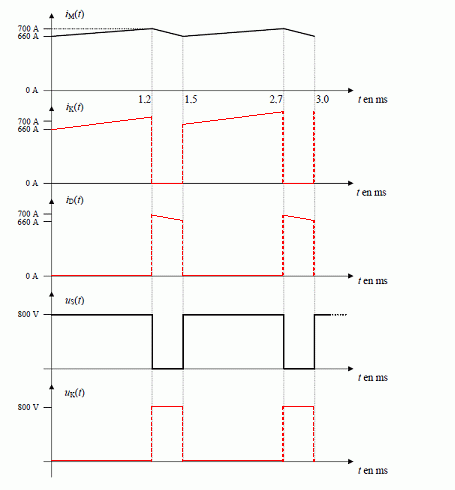
Donner la période TH
de hachage et en déduire la fréquence fH de ce hachage.
TH = 1,5 ms = 1,5 10-3
s ; fH = 1/TH = 1/ 1,5 10-3= 667 Hz.
Déterminer
le rapport cyclique a de ce
hacheur.
a = 1,2 / 1,5 = 0,8.
Exprimer
littéralement ( sans justifier ) la valeur moyenne <uS>
de la tension uS(t) en fonction de a et E0 puis la calculer.
<uS> a E0 = 0,8 *800 =
640 V.
On néglige la résistance de la bobine.
Montrer
que <uM> ~ <uS>.
uM +uL = uS ; uL =LdiM/dt
; <uM > +L<diM/dt > = < uS>.
Or iM est une fonction périodique ; la moyenne de sa dérivée
<diM/dt > est donc nulle ; par suite : <uM>
~ <uS>.
Déterminer
le rapport cyclique aN au régime nominal
permettant d'obtenir : <uM> = 760 V.
aN E0
= 760 ; aN = 760
/ E0 = 760 / 800 = 0,95.
Etude
de l'électronique de commande.
On donne le schéma d'une partie de l'électronique de commande
permettant la régulation de vitesse du moteur.
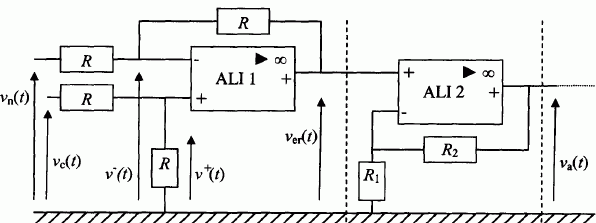
La tension vc(t)
est une tension de consigne permettant de régler la valeur de la
vitesse du moteur. La tension vn(t) provient d'un capteur de
vitesse et est liée à celle-ci par la relation suivante : vn(t)
=0,010 n avec n exprimée en tour / min. Les amplificateurslinéaires
intégrés idéaux ( ALI 1 et ALI 2 encore appelés amplificateurs
opérationnels ) sont alimentés par des tensions symétriques +15 V / -15
V. Le premier étage réalise la fonction " opération de différence". Le
second permet d'amplifier la tension ver(t).
Montrer
que les ALI 1 et ALI 2 peuvent fonctionner en
régime linéaire.
Il
existe entre l'entrée inverseuse et la sortie une boucle de
contre-réaction. Les amplificateurs opérationnels peuvent donc
fonctionner en régime linéaire.
En
justifiant, montrer que la tension v+(t) est égale à ½vc(t).
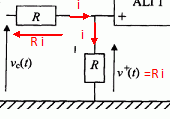
L'intensité dans
l'entrée non inverseuse de l'AO est nulle.
vc(t) = Ri + Ri et v+(t) = Ri d'où : vc(t)
= 2 v+(t) soit v+(t) =½vc(t).
On a v-(t) = ½[ vn(t) + ver(t) ].
En déduire une
relation entre ver(t), vc(t) et vn(t).
En régime linéaire : v+(t) = v-(t)
; ½vc(t) = ½[ vn(t) + ver(t) ] d'où vc(t)
= vn(t) + ver(t).
Montrer que va(t)
= (R1+R2) / R1 ver(t).
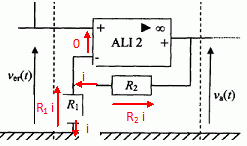
va(t) = R1
i + R2 i et ver(t) = R1 i soit i = ver(t)
/ R1 ;
va(t) =(R1 +R2) ver(t) / R1.
Sachant que R1 = 10 kW, calculer la valeur de R2 pour avoir va(t) = 5,7 ver(t).
va(t) =(R1 +R2) ver(t) / R1 et va(t) = 5,7 ver(t).
par suite : (R1 +R2) / R1 = 5,7 ; R1 +R2 = 5,7 R1 ; R2 = 4,7 R1 = 47 kW.
|
Etude de la régulation de vitesse.
Le
schéma ci-dessous présente la boucle de régulation de la vitesse du
moteur en commandant sa fréquence de rotation. On suppose que la
tension va agit par l'intermédiaire du hacheur de manière à avoir n = 200 va avec n exprimée en tr/min.
On connaît par ailleurs va= 5,7 ver et vn = 0,010 n (exprimée en tr/min).
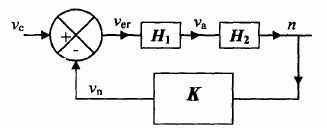
Donner la valeur respective des transmittances K, H1 et H2 sans oublier les unités.
K = vn / n ( V min tr-1) ; H1 =va / ver ( sans unité) ; H2 =n /va ( tr min-1 V-1).
Comment s'appelle la partie de la boucle correspondant à la transmittance K ?
C'est une chaine de retour.
Exprimer la transmittance H de la chaine directe en fonction de H1 et H2, puis la calculer.
H = H1 H2 = va / ver n /va =n / ver = 200*5,7 =1140.
Montrer que la transmittance de la boucle fermée s'écrit : T = n / vc = H / (1+KH).
ver = vc-vn ; vn = Kn ; ver = n /H;
n /H = vc-Kn ; vc= n / H +Kn = n [1+KH) / H.
Par suite : T = n / vc = H / (1+KH).
Calculer T.
T = 1140 / (1 + 0,010*1140) =91,93 ~ 92 tr min-1 V-1.
Déterminer la valeur de vc permettant d'avoir n = 1125 tr/min.
vc =n / T = 1125 / 91,93 =12,2 V.
|





