|
QCM
Sachant
que l'énergie de liaison du noyau de xénon 129 vaut 1087 MeV et que
celle du noyau de cobalt 60 vaut 526 MeV, on peut en conclure que le
noyau de xénon 129 est plus stable que le noyau de cobalt 60. Faux.
Energie de liaison par nucléon : xénon 129 : 1087 / 129 =8,42 MeV/ nucléon.
cobalt 60 : 526 / 60 =8,77 MeV/ nucléon, valeur supérieure à 8,42 : le noyau de cobalt 60 est plus stable que le noyau de énon 129.
Dans
une désintégration radioactive, si la différence entre l'énergie de
masse du noyau père et la somme des énergies de masse du noyau fils et
de la particule vaut 4,0 MeV, on peut en conclure que cette énergie de
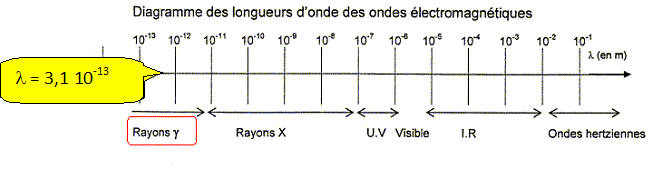
4,0 MeV est emportée par un rayon g. Vrai.
E =4,0 MeV = 4,0 * 1,6 10-13 J =6,4 10-13 J.
E = h c/l ; l = hc/E =6,67 10-34 *3 108 / 6,4 10-13 =3,1 10-13 m.
Les réactions de fusion nucléaire sont à l'origine de l'énergie libérée par le soleil. Vrai.
Dans la réaction nucléaire : 63Li +21H--->2AZX, le noyau noté X est le noyau de bérylium 84Be. Faux.
Conservation de la charge : 3+1 = 2 Z d'où Z = 2 ( élément hélium He)
Conservation du nombre de nucléons : 6+2 = 2A d'où A = 4.
63Li +21H--->242He.
|
La réaction nucléaire : 23592U +10n--->9140Zr +14258Ce +310n +60-1e.
est une réaction de fission. Vrai.
Le noyau d'uranium 235 conduit à deux noyaux fils.
Il n'y a aucune énergie de liaison dans le noyau d'hydrogène 11H. Vrai.
Ce noyau est constitué d'un seul nucléon.
|
Fission de l'uranium.
Calculer l'énergie de liaison d'un noyau de lanthane 13957La ainsi que son énergie de liaison par nucléon.
On donne : masse du noyau de lanthane 139 : mLa =2,306 20 10-25 kg ;
masse d'un proton ; mP =1,672 6 10-27 kg ; masse d'un neutron : mN =1,674 9 10-27 kg.
Ce noyau compte 57 protons et 139-57 = 82 neutrons.
Energie de liaison : Dm= 82* mN +57mP -mLa =82 *1,674 9 10-27 +57*1,672 6 10-27 -2,306 20 10-25 ;
Dm=1,37342 10-25 +9,5338 10-26 -2,306 20 10-25 =2,0602 10-27 kg.
E = Dm c2 =2,0602 10-27 (3 108)2 =1,854 10-10 J.
Energie de liaison par nucléon : 1,854 10-10 / 139 =1,3338 10-12 J / nucléon =1,3338 10-12 / 1,6 10-13 MeV/nucléon =8,34 MeV/nucléon.
On donne la courbe d'Aston :
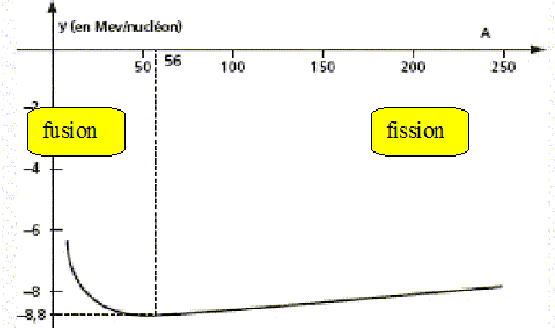
D'après la courbe, indiquer quelles réactions, parmi le 4 envisagées, sont susceptibles de fournir de l'énergie.
- fusion de deux noyaux légers. (vrai)
- fission d'un noyau léger. ( faux )
- fusion de deux noyaux lourds ( faux)
- fission d'un noyau lourd. ( vrai). On admet que la courbe d'Aston peut être assimilée à une droite d'équation y = lA +µ pour les noyaux dont le nombre de nucléons est supérieur à 80.
l = 7,226 10-3 MeV/nucléon2 ; µ =-9,281 MeV/nucléon.
Calculer la valeur de l'énergie de liaison par nucléon pour le lanthane 139. Conclure.
y =7,226 10-3 *139 -9,281 = -8,27 MeV/nucléon.
Energie de liaison par nucléon du lanthane 129 : 8,27 MeV/nucléon.
Ecart relatif avec la valeur calculée ci-dessus : (8,34-8,27) / 8,3 = 8,4 10-3 ( 0,8 %)
Les valeurs trouvées sont compatibles.
|
Lors
d'une réaction de fission, un noyau d'uranium 235 heuté par un neutron
se casse en deux noyaux fils, comportant respectivement 95 et 139
nucléons.
On
admet que l'énergie libérée est égale à la différence entre la somme
des énergie de liaison des deux noyaux fils et l'énergie de liaison de
l'uranium 235.
Evaluer en MeV, l'énergie libérée par la fission d'un noyau d'uranim 235.
ylanthane =7,226 10-3 *139 -9,281 = -8,27 MeV/nucléon.
Energie de liaison : Elanthane =8,27*139 =1,15 103 MeV.
yfils =7,226 10-3 *95 -9,281 = -8,595 MeV/nucléon.
Energie de liaison : Efils =8,595*95 =8,16 102 MeV.
yuranium =7,226 10-3 *235 -9,281 = -7,58 MeV/nucléon.
Energie de liaison : Euranium =7,58*235 =1,78 103 MeV.
Energie libérée : Elanthane + Efils -Euranium =1,15 103 +8,16 102 -1,78 103 =1,84 102 MeV.
Vérifier l'affirmation suivante : la fission d'un gramme d'uranium libère une énergie voisine de 1 MW jour.
Nombre de noyaux d'uranium 235 dans 1 g :
1 /235 * 6,02 1023 =2,56 1021.
Energie lbérée par la fission de ces noyaux :
2,56 1021 * 184 =4,71 1023 MeV = 4,71 1023 *1,6 10-13 J =7,54 1010 J =7,54 104 MJ.
1 jour = 24*3600 s = 8,64 104 s.
7,54 104 / 8,64 104 ~ 0,9 MW jour.
|
|

