Le
moteur thermique étant très certainement appelé à disparaître, les
constructeurs automobiles recourront probablement au "tout électrique"
ou à une motorisation hybride mettant en jeu une pile à
combustible.
Le but de cet exercice est d'étudier d'une part le supercondensateur
pouvant intervenir dans ces deux types de véhicules et d'autre part, la
pile à combustible.
Etude du supercondensateur.
Un
supercondensateur permet de stocker une quantité d'énergie beaucoup
plus élevée qu'un condensateur électrolytique classique. Il permet de
plus de la restituer plus rapidement qu'un accumulateur électrochimique.
Les caractéristiques du supercondensateur étudié, donnée à 25°C sont :
capacité C = 2600 F ; tension nominale : 2,7 V ; masse m = 500 g ;
énergie massique du condensateur chargé sous une tension de 2,7 V : 19
kJ kg-1.
Charge du condensateur à courant constant.
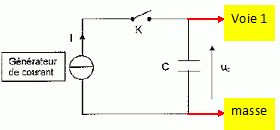
On réalise le circuit ci-dessous. A l'instant t=0, on ferme
l'interrupteur k. On charge alors ce condensateur à l'aide d'un
générateur de courant qui permet de délivrer une intensité constante I=
10 A puis on ouvre l'interrupteur à la date t1. Un système d'acquisition permet de visualiser la tension uC aux bornes du condensateur en fonction du temps.
EIndiquer les branchements à réaliser pour visualiser la tension aux bornes du condensateur.
|
|
Exprimer uC en fonction de C et de la charge q du condensateur.
q = CuC.
Exprimer t en fonction de C, uC et I lorsque t est inférieur ou égal à t1.
q = It, l'intensité est constante
CuC= It ; t = CuC / I. |
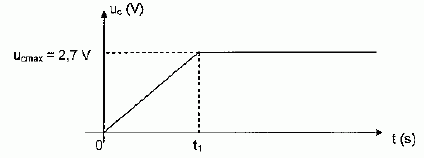
Calculer t1.
t1= 2600 *2,7 / 10 =702 s ~7,0 102 s.
Exprimer puis calculer l'énergie emmagasinnée par le condensateur lorsque la tension à ces bornes est 2,7 V.
E = ½CuC2 = 0,5*2600*2,72 =9477 J ~9,5 kJ.
Le résultat est-il en accord avec les caractéristiques données par le fabricant ? Justifier.
masse du condensateur : m = 0,5 kg
Energie stockée par kilogramme : 9477 / 0,5 = 18954 J kg-1 ~ 19 kJ kg-1.
Accord avec les données.
Décharge du condensateur.
Le condensateur étant chargé sous une tension de 2,7 V, on réalise le
circuit suivant pour étudier sa décharge à travers un conducteur
ohmique de résistance R = 1,0 ohm.
A l'instant t=0, on ferme l'interrupteur K. On visualise, à l'aide d'un système d'acquisition, l'évolution de la tension uC aux bornes du condensateur en fonction du temps.
Représenter les tensions uC aux bornes du condensateur et uR aux bornes du conducteur ohmique.
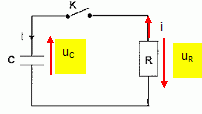
Etablir l'équation différentielle vérifiée par uC, donnée ci-dessous : RC duC/dt + uC=0.
Additivité des tensions : uC + uR = 0 avec uR = R i et i = dq/dt = CduC/dt.
uc +RCduC/dt =0
Par une équation aux dimensions, montrer que RC est homogène à un temps.
R a la dimension d'une tension divisée par une intensité : [R] = [U]
[I]-1.
q = C U et dq= i dt ; C = q / U : [C] = [I] [T]
[U]-1.
par suite : [R C] = [T].
La solution de l'équation différentielle est de la forme uC = A+ B exp(-t / (RC) où A et B sont des constantes.
A partir de la condition initiale, trouver une relation entre A et B.
Le condensateur est initialement chargé sous la tension uC = 2,7 V.
2,7 = A + B exp(-0) ; 2,7 = A+B.
Quelle est la valeur de uC lorsque le condensateur est déchargé ?
La tension aux bornes d'un condensateur déchargé est nulle.
En déduire les valeurs de A et de B.
uC(infini) = 0 = A+B exp(-infini) = A, d'où A = 0.
Par suite B = 2,7 V.
On donne graphiquement l'évolution de la tension uC au cours du temps.
Déterminer graphiquement la constante de temps du circuit. Vérifier cette valeur par le calcul.
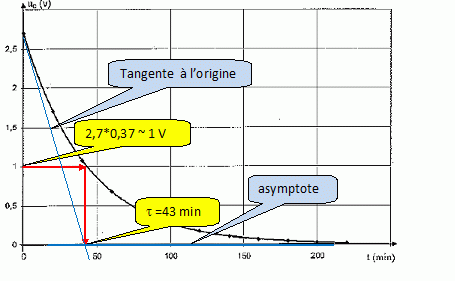
t = RC avec R = 1,0 ohm et C = 2600 F ; t = 1,0*2600 = 2600 s = 43 min.
Eude d'une pile à combustible.
Une pile à combustible ( PAC) est un assemblage de cellules
élémentaires, comprenant deux électrodes contenant un catalyseur ( le
plus souvent du platine), séparées par un électrolyte, dont le rôle est
de permettre la migration des ions d'une électrode à l'autre.
Le comburant est du dioxygène. le combustible est le plus souvent du
dihydrogène. Ce combustible gazeux à température ambiante et
inflammable, pose des problèmes de stockage.
Un autre combustible possible est le méthanol. Ce combustible est
certes toxique, mais liquide à température ambiante. Il est produit
principalement à partir du gaz naturel. On se dispense ainsi du
problème de stockage du dihydrogène. Une telle pile à combustible
est appelée DMFC ( Direct Methanol Fuel Cells). L'électrolyte utilisé
est acide.
La température est fixée à 298 K ; M(H) = 1,0 ; M(O) = 16,0 ; M(C) = 12,0 g/mol ; NA = 6,02 1023 mol-1 ; e = 1,6 10-19 C : masse volumique du méthanol r = 0,79 g / mL.
La pile débite un courant à travers un dipôle ohmique de résistance R.
|
L'équation associée à la réaction lorsque la pile débite est :
2CH3OHaq + 3 O2(g) = 2CO2(g) + 4 H2O(l).
Les couples oxydant / réducteur mis en jeu sont : CO2(g) / CH3OHaq ; O2(g) / H2O(l)
Ecrire
les demi-équations électroniques rendant compte des transformations se
produisant à chaque élctrode. Préciser à quelle électrode a
lieu chaque réaction et préciser s'il s'agit d'une oxydation ou d'une réduction.
Une réduction se produit à la cathode positive :
O2(g) + 4H+aq + 4e- = 2 H2O(l).
Une oxydation se produit à l'anode négative :
CH3OH aq + H2O(l)= CO2(g) + 6H+aq + 6e-
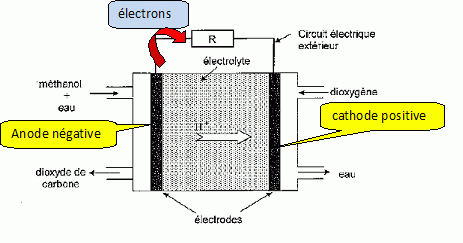
Indiquer
la polarité des électrodes sur le schéma, le sens de circulation des
électrons dans le circuit extérieur, lorsque la pile fonctionne.
La pile débite un courant I = 50 mA pendant 2,0 h.
Exprimer puis calculer le nombre de mole d'électrons ne transférés spontanément pendant cette durée puis la calculer.
Quantité d'électricité Q = I Dt ;
La charge, en valeur absolue, d'une mole d'électrons est NA e = 1 F :
par suite : Q = I Dt = NA e ne d'où ne = I Dt /( NA e).
I = 0,05 A ; Dt = 2,0*3600 = 7200 s ; ne= 0,050*7200 / ( 6,02 1023 x 1,6 10-19 ) =3,74 10-3 ~3,7 10-3 mol.
Exprimer puis calculer le volume de méthanol consommé.
CH3OH aq + H2O(l)= CO2(g) + 6H+aq + 6e-
Les nombres stoechiométriques conduident à : n(méthanol) = ne / 6.
Masse molaire du méthanol M = 12+4+16 = 32 g/mol
masse de méthanol : m = M n(méthanol) = M ne / 6 grammes
volume ( mL) = masse (g) / masse volumique ( g/mL)
V = m / r = M ne / (6 r).
V = 32*3,74 10-3 /(6*0,79) = 2,5 10-2 mL.
|




