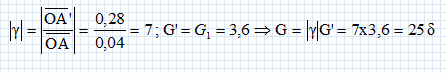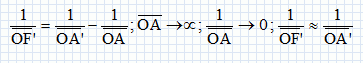François-Maël
et Anne-Claire sont deux enfants curieux. En rentrant de l’école, ils
se rendent compte que la pelouse regorge de sauterelles. Ils
entreprennent alors d’en capturer quelques unes afin de les observer.
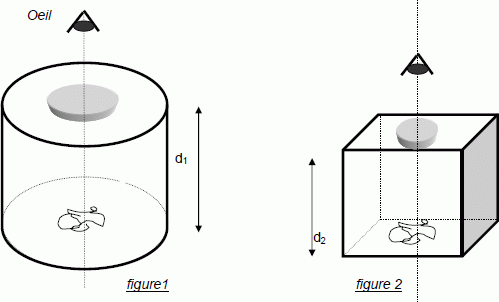
Pour observer les sauterelles capturées, les deux enfants disposent de deux systèmes :
- un gobelet transparent d’une profondeur définie d1 = 7,0 cm (figure 1), muni d’une loupe sur la partie supérieure ;
- d’un compte-fils constitué d’une autre loupe montée sur un support à distance connue d2 =3,5 cm d’un plan d’observation transparent (figure 2).
Les deux « systèmes » optiques sont conçus pour que les apprentis
observateurs puissent voir les images sans que leurs yeux aient à
accommoder.
Etude des deux lentilles.
Que représentent, d’un point de vue optique, les deux distances d1 et d2 ?
On considère que l’oeil n’accommode pas lorsqu’il regarde à l’infini.
L'image de l'objet réel se trouve à l'infini. L'objet se trouve dans le
plan focal objet de la lentille convergente. La distance d1 ( ou d2 ) représente la distance focale de la lentille.
|
Le grossissement d’une loupe est donné par la relation : G =1 / (4f' ) où f’ représente la distance focale de la loupe.
Calculer les grossissements G1 et G2
des deux loupes utilisées par les jeunes observateurs. Avec laquelle de
ces deux loupes, la sauterelle capturée sera-t-elle vue plus grosse ?
G1 = 1/(4d1) = 1/ (4*0,070) = 3,6 m-1 (ou dioptrie).
G2 = 1/(4d2) = 1/ (4*0,035) = 7,1 m-1 (ou dioptrie).
La sauterelle observée est plus grosse avec le compte-fils.
|
Une technique pour augmenter le grossissement.
Les deux enfants ne sont dans un premier
temps que partiellement satisfaits de leurs observations. Anne-Claire
demande : « Comment pourrait-on voir plus gros la sauterelle ? »
« Et si on mettait l’un des systèmes au-dessus de l’autre ? » suggère François-Maël.
Le plus simple pour eux est de placer le compte-fils sur le gobelet et
d’observer la sauterelle à travers ce dispositif. En plaçant l’oeil
près du compte-fils, ils voient « flou » mais lorsqu’ils se placent à
une grande distance, ils voient leur insecte net, à l’envers, mais plus
petit qu’en réalité.
Après discussion, les deux enfants décident d’inverser les deux
systèmes. Après quelques essais, ils constatent que pour voir la
sauterelle nettement plus grosse, ils doivent placer le
compte-fils de telle sorte que sa lentille soit située à une distance D = 4,0 cm de la sauterelle sans avoir à accommoder.
Instrument d’optique construit par les enfants :
Quel
instrument d’optique, correspondant à leur souhait, les deux enfants
ont-ils construit ?Comment appelle-t-on chacune des deux lentilles,
dans cet instrument d’optique ?
Les enfants ont construit un microscope. La lentille la plus proche de
la sauterelle est l'objectif ; la lentille la plus proche de l'oeil est
l'oculaire.
Calculer
la position de l’image intermédiaire donnée par la lentille la plus
proche de l’objet en utilisant la formule de conjugaison.
" sans
avoir à accommoder" : l'image définitive se forme à l'infini ; l'image
intermédiaire A'B' est dans le plan focal image de l'oculaire.
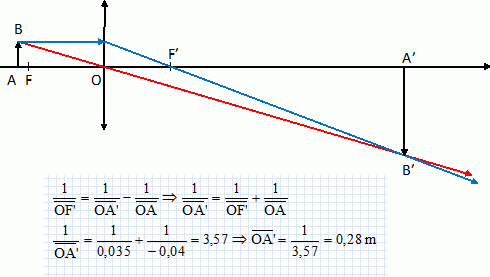
Construire à l’échelle ½ horizontalement, la situation optique créée par les enfants.
La sauterelle sera représentée par une flèche verticale AB de 1 cm posée sur l’axe principal (échelle 1verticalement).
On rappelle que spontanément les enfants se placent de telle sorte que
leurs yeux n’accommodent pas ; l’image définitive est à l’infini.
Le grossissement de l’instrument ainsi construit est donné par la relation G = |g| .G’ où g représente le grandissement de la lentille devant l’objet et G’ le grossissement
de la seconde lentille.
Calculer
alors le grossissement de l’instrument et justifier le fait que les
enfants trouvent la sauterelle observée beaucoup plus grosse.
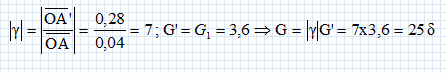
G est supérieur à G2 : l'image de la sauterelle est bien plus grande.
L'antenne TV apparaît plus grosse.
En rangeant les deux systèmes, Anne-Claire pose le compte-fils sur le gobelet et se met à
observer vers le ciel avec l’ensemble. « Oh ! je vois l’antenne TV des voisins à l’envers et plus grosse ! » s’exclame-t-elle.
Quel instrument d’optique connu vient de construire la fillette ?
Une lunette terrestre afocale ( obbjet à l'infini et image définitive à l'infini ).
Où se
forme l’image intermédiaire dans cette situation, en supposant que
l’antenne est très éloignée de l’instrument ? Justifier à l’aide de la
formule de conjugaison.
L'image intermédiaire d'un objet réel, situé à l'infini, se forme au foyer image de l'objectif, le gobelet.
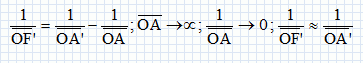
La construction permettant d’obtenir l’image définitive de l’antenne est fournie ci dessous :
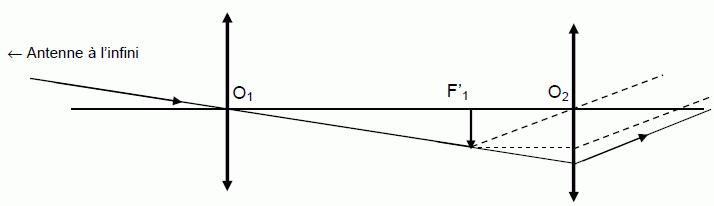
|
Dans ces conditions d’observation, où se situe le foyer objet de la lentille L2 ?
L'image définitive est à l'infini ; l'image intermédiaire, jouant le rôle d'objet pour L2, se trouve donc au foyer objet de L2.
Démontrer que le grossissement de cet instrument est G=f'1 / f'2.
f ’1 représente la distance focale de l’objectif et f ’2 la distance focale de l’oculaire.
Faire l’application numérique.
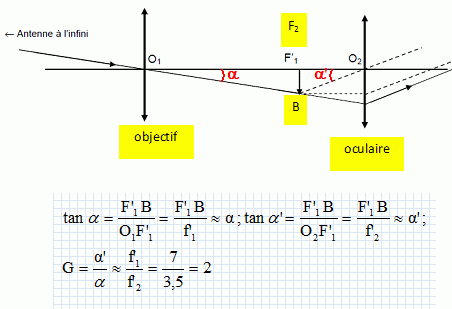
Dans l'hypothèse des angles petits, on peut confondre la tangente et l'angle exprimé en radian.
|
|