Oscillations chimiques :
La
réaction de Briggs et Rauscher est une réaction chimmique oscillante.
Lorsqu'on mélange les différents réactifs la solution passe
alternativement du jaune au bleu. la réaction est complexe. Cependant
on peut considérer que le bilan est une réaction de dismutation du
peroxyde d'hydrogène H2O2 ( ou eau oxygénée).
2H2O2 aq = 2H2O(l) + O2(g) (1).
Le peroxyde d'hydrogène intervient en tant qu'oxydant dans le couple H2O2 aq /H2O(l).
Quel est l'autre couple oxydant /réducteur mis en jeu ? Quel est le rôle du peroxyde d'hydrogène dans cet autre couple ?
Le peroxyde d'hydrogène joue le rôle de réducteur dans le couple : O2(g) /H2O2 aq.
On peut expliquer de façon simple le phénomène en distinguant deux
phases principales qui se répètent et qui mettent en jeu un
second réactif, l'acide iodique HIO3.
5H2O2 aq +2HIO3 aq = 5 O2(g) +I2aq +6H2O(l) (2)
puis : I2aq +5H2O(l) = 2HIO3 aq +4H2O(l) (3).
Lors de la réaction 2, il y a apparition de diiode qui, en présence
d'empois d'amidon, conduit à la formation d'un complexe bleu. Lors de
la réaction 3, il y a disparition du diiode d'où la disparition de la
coloration bleue.
Le mélange initial a été réalisé en utilisant un volume V1 = 20 mL d'une solution aqueuse de peroxyde d'hydrogène de concentration molaire en soluté apporté c1 = 4,5 mol/L et un volume V2 = 20 mL d'une solution aqueuse préparée à partir d'une masse m2 d'acide iodique égale à 0,70 g.
Calculer les quantités de matière initiales de H2O2 et de HIO3.
n( H2O2) =c1V1 =4,5*0,020 = 9,0 10-2 mol.
n(HIO3) = m2 / M avec M = 1+126,9+3*16 = 175,9 g/mol ; n(HIO3) = 0,70 / 175,9 =3,98 10-3 ~4,0 10-3 mol.
|
Déterminer le réactif limitant et l'avancement maximal.
|
avancement (mol)
|
5H2O2 aq |
+2HIO3 aq |
= 5 O2(g) |
+I2aq
|
+6H2O(l) |
début
|
0
|
0,09
|
0,004
|
0
|
0
|
solvant
|
en cours
|
x
|
0,09-5x
|
0,004-2x
|
5x
|
x
|
large
|
fin
|
xmax
|
0,09-5xmax |
0,004-2xmax |
5xmax |
xmax |
excès
|
si H2O2 aq est en défaut : 0,09-5xmax=0 ; xmax= 0,09/5 =0,018 mol
si HIO3 aq est en défaut : 0,004-2xmax= 0 ; xmax= 0,004/2 =0,002 mol
HIO3 aq est donc en défaut.
|
En déduire la concentration maximale de diiode qui peut se former sachant que le volume total est 60 mL.
[I2aq] = xmax / Vtotal = 0,002 / 0,060 =3,3 10-2 mol.
L'évolution de la réaction peut être suivie par spectrophotométrie.
Quelle est la grandeur mésurée par un spectrophotomètre ?
Un spectrophotomètre mesure l'absorbance A.
Pour suivre les variations de la concentration du complexe bleu formé
lors de la réaction 2 en fonction du temps, le spectrophotomètre est
réglé sur une longueur d'onde dans le vide égale à 600 nm, dans le
domaine du jaune.
Justifier ce choix.
La
solution est bleue ; elle absorbe la couleur complémentaire du bleu,
c'est à dire le jaune. La longueur d'onde choisie doit correspondre au
maximum d'absorption.
L'étude a permis de tracer la courbe suivante :
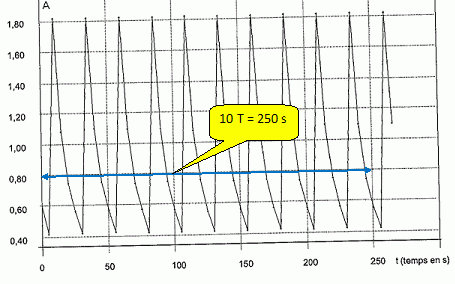
T = 25 s ; fréquence = 1/T = 1/25 = 0,040 Hz.
Pour une concentration en diiode de 2,50 10-3 mol/L, la valeur de A est 1,03. On admettra que la concentration en diiode formé est égale à celle du complexe coloré.
Déterminer la concentration molaire maximale du diode dans le milieu réactionnel. Comparer à la valeur précédente et conclure.
L'absorbance et la concentration en diiode sont proportionnelles.
Valeur maximale de l'absorbance : 1,80 ( lecture graphe ).
[I2aq]max = 1,80 / 1,03 *2,50 10-3 =4,37 10-3 mol/L.
Cette valeur est environ 8 fois plus petite que celle calculée
ci-dessus. La valeur calculée précédemment correspondait à une
réaction (2) supposée totale.
La valeur expérimentale permet de conlure que la réaction (2) n'est pas totale.
Oscillations mécaniques.
Les frottements sont négligés.
On peut modéliser un oscillateur mécanique horizontal par un système
solide-ressort constitué d'un solide (S) de masse m, mobile sur un rail
à coussin d'air, fixé à l'extrémité d'un ressort à spires non
jointives, de masse négligeable et de constante de raideur k. La
position du centre d'inertie du solide est étudiée dans un référentiel
terrestre considéré comme galiléen et repéré par son abscisse x(t) sur
un axe horizontal x'Ox. L'origine des abscisse s O correspond à
l'abscisse de G lorsque le solide est à l'équilibre. Ecarté de sa
position d'équilibre puis lâché sans vitesse initiale à t=0, le solide
(S) oscille.
Nommer les forces extérieures appliquées à (S) et les représenter.
Le solide est soumis à son poids, à l'action du banc et à une force de rappel exercée par le ressort.
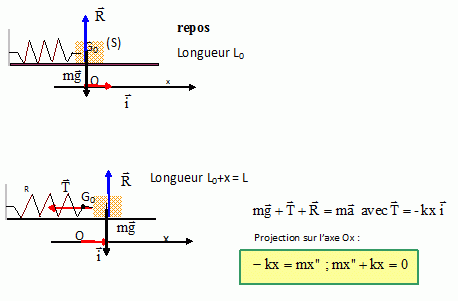
Quelle loi faut-il appliquer au solide (S) pour déterminer son accélération ?
On applique la seconde loi de Newton.
L'équation différentielle s'écrit : x" + k/m x = 0.
Vérifier que x(t) = Xmax cos (2pt/T) est solution de cette équation si T = 2p(m/k)½.
x'(t) = -Xmax 2p/T sin (2pt/T)
x"(t) = -Xmax (2p/T )2 cos (2pt/T) = -(2p/T )2 x(t).
Repport dans l'équation différentielle : -(2p/T )2 x(t) + k/m x(t) = 0.
cette équation est vérifiée quelque soit le temps si : (2p/T )2 = k/m soit T = 2p(m/k)½.
|
Détermination de la masse d'un astronaute.
Comment se peser dans une navette spatiale où règne l''apesanteur ?
L'utilisation d'un pèse personne n'étant pas possible, les
scientifiques ont utilisé le dispositif de la chaise oscillante : un
siège de masse m mobile sur un rail à coussin d'air est fixé à
l'extrémité d'un ressort, l'autre extrémité étant relié à un point fixe
de l'engin spatial.
La période propre T1 des oscillations de la chaise " à vide" est égale à 1,28 s.
Lorsque l'astronaute, de masse M, est arrimé sur la chaise, la période propre T2 est égale à 2,39 s.
Donner l'expression de T1 et T2 puis vérifier que M = [(T2/T1)2-1] m.
T1 = 2p(m/k)½ ; T2 = 2p((M+m)/k)½ ;
T21 = 4p2(m/k) ; T22 = 4p2((M+m)/k) ;
T22 / T21 =M/m+1 ; M = [(T2/T1)2-1] m.
A.N : m = 25,2 kg
M = 25,2 [(2,39 / 1,28)2-1] =62,7 kg.
|
|

