Propagation
d'une onde sur une corde
On
étudie la propagation de signaux transversaux le long d'une corde
élastique tendue horizontalement. On a crée un signal transversal à
chaque extrémité ( en la soulevant puis en l'abaissant ). Les deux
signaux se propagent d'abord l'un vers l'autre,se superposent puis
s'éloignent l'un de l'autre : les sens de propagation sont indiqués par
des flèches sur la figure qui reproduit, en vraie grandeur, des
photographies de la corde à différents instants notés t1, t2,
t3, t4.
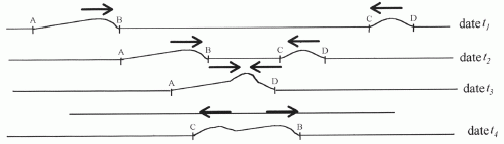
La durée
séparant les clichés 1 et 2 vaut : (t2-t1)
=5,0 ms.
Déterminer la célérité des ondes le long de la corde.
Le
point C se déplace de 4,0 cm en 5,0 ms : v = 4,0 10-2 / 5,0
10-3 = 8,0 m/s.
En déduire les durées t3-t1 et t4-t1.
Le point C se déplace de
6,0 cm en ( t3-t1
) à la célérité v = 8,0 m/s : t3-t1
=0,060 / 8,0 = 0,0075 s = 7,5 ms.
Le point D se déplace de 8,0 cm en ( t4-t1
) à la célérité v = 8,0 m/s : t4-t1
=0,080 / 8,0 = 0,010 s = 10 ms.
|
On
relie l'une des extrémités de la corde à un vibreur qui impose, à cette
extrémité, des oscillations sinusoïdales. On observe alors la
propagation d'une onde transversale le long de la corde.
Calculer
la longueur d'onde l si la
fréquence du vibreur est 50 Hz.
l =
v / f =8,0 / 50 = 0,16 m.
Lors des expériences précédentes, la tension de la corde valait F =
15,0 N. Sachant que la célérité de propagation des ondes est
proportionnelle à la racine carrée de la tension, calculer la longueur
d'onde si l'on choisit pour la tension F' = 20,0 N en conservant la
même fréquence du vibreur.
v = k F½ avec k une constante.
v = 8,0 = k 15½d'où k = 2,066 S.I
v' =
k F'½ =2,066*20½ =9,24 m/s ; l' =v'/f = 9,24 / 50 =0,18
m.
|
Ondes sismiques
A
2400 km de l'épicentre d'un séisme, les sismographes enregistrent avec
un retard de 6 min 40 s, des vibrations de fréquence f = 1,0 Hz.
Calculer
la longueur d'onde.
Dt = 6*60 + 40 = 400 s ; d = 2400 km = 2,4 106 m ; célérité v = d / Dt = 2,4 106 / 400 =6,0 103 m/s.
l = v / f = 6,0 103 / 1,0 = 6,0 103 m.
Ondes sur un
ressort.
La
figure ci-dessous reproduit en vraie grandeur la photographie d'un
ressort dont l'une des extrémités est reliée à un vibreur de fréquence
f = 100 Hz.

S'agit-il d'ondes transversales ou longitudinales ? Quelle est la longueur d'onde ?
La déformation du ressort se propage dans la même direction que la propagation de l'onde : donc ondes longitudinales.
Longueur d'onde = distance séparant deux zones de compression successives.

Déterminer la vitesse de propagation de l'onde.
v = l f = 5,0 10-2 *100 = 5,0 m/s.
Echelle de perroquet.
La
figure ci-dessous reproduit la photographie d'une echelle de peroquet
horizontale dont l'extrémité est animée d'un mouvement sinusoïdal de
période t = 0,85 s.
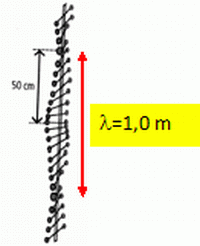
S'agit-il d'ondes transversales ou longitudinales ? Quelle est la longueur d'onde ?
La déformation de l'échelle est perpendiculaire à la direction que la propagation de l'onde : donc ondes transversales.
Longueur d'onde = distance séparant deux zones " immobiles" successives.
Déterminer la vitesse de propagation de l'onde.
v = l f = l / T = 1,0 / 0,85 = 1,176 ~ 1,2 m/s.
|
Ondes sonores.
Un
haut parleur émet un son sinusoÏdal. Les ondes reçues par deux
microphones séparéés par une distance d = 34 cm sont reçues par un
oscilloscope réglé sur une base de temps de 0,20 ms / division.
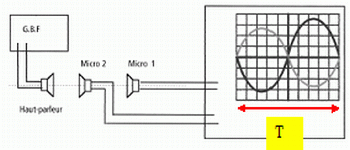
Déduire de l'enregistrement la fréquence du son émis puis sa longueur d'onde dans l'air.
Une période correspond à 10 divisions soit à 10*0,2 = 2,0 ms = 2,0 10-3 s.
fréquence f = 1/T = 1/ 2,0 10-3 = 500 Hz.
On observe deux signaux en opposition de phase : les deux microphones sont distants d'un nombre impair de demi-longueur d'onde.
½(2n+1) l = 0,34 avec n entier.
l = 0,68 / (2n+1).
La célérité du son dans l'air est v ~ 340 m/s à température ambiante.
l = v / f =340/500 =0,68 m.
|




