Les ondes sonores : bac S Liban 2010

Membre d'un groupe de rock et très interessé par la nature et la propagation du son, Julien réalise les observations suivantes : - Observation 1 : aucun signal sonore ne nous parvient du Soleil alors qu'il s'y déroule en permanence de gigantesques explosions. - Observation 2 : une bougie est placée devant un haut parleur qui émet un son très grave. On constate que la flamme se rapproche et s'éloigne alternativement de la membrane du haut-parleur mais qu'elle n'oscille pas dans la direction perpendiculaire. Préliminaires. Définir une onde mécanique progressive. On appelle onde mécanique progressive le phénomène de propagation d'une perturbation dans un milieu matériel sans transport de matière, mais avec transport d'énergie. Une onde se propage, à partir de la source, dans toutes les directions qui lui sont offertes.  Compléter les cases du tableau avec les expressions suivantes : onde sonore, onde le long d'une corde, onde lors de la compression- dilatation d'un ressort, onde à la surface de l'eau. ondes à une dimension ondes à 2 dimensions ondes à 3 dimensions onde longitudinale onde lors de la compression- dilatation d'un ressort onde sonore onde transversale onde le long d'une corde onde à la surface de l'eau Célérité de l'onde sonore : première méthode. Trois microphones M1, M2 et M3 sont alignés de telle manière que les distances M1M2 et M2M3 valent respectivement 2,00m et 3,00 m. Les sigaux électriques correspondant aux sons reçus par les microphones sont enregistrés grâce à un ordinateur. Julien donne un coup de cymbale devant le premier micro, puis lance immédiatement l'enregistrement. La température de la pièce est de 18 °C. Les courbes obtenues sont représentées ci-après : A l'instant t, la position du solide est repérée par l'abscisse x(t) sur l'axe : x(t) représente également l'allongement du ressort. Un dispositif d'acquisition a permis d'obtenir l'enregistrement ci-dessous.   Comment peut-on déterminer la célérité de l'onde ? 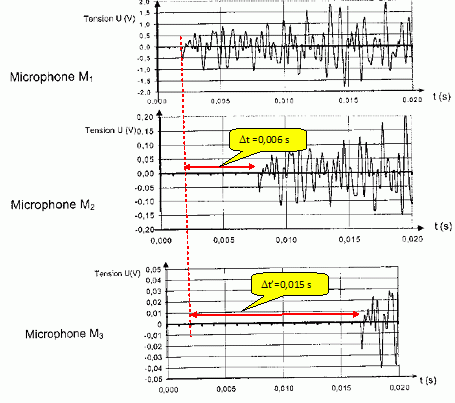c = M1M2 / Dt = 2,00 / 0,006 = 333 ~3,3 102 m/s. c = M1M3 / Dt' = 5,00 / 0,015 = 333 ~3,3 102 m/s. c = M2M3 / (Dt' - Dt) = 3,00 / 0,09 = 333 ~3,3 102 m/s. Les résultats sont cohérents. Célérité de l'onde sonore : deuxième méthode. Julien dispose maintenat les deux microphones M1 et M2 à la même distance d d'un diapason. Il obtient les courbes représentées ci-dessous. On remarque que les signaux sont en phase. Déterminer la période puis la fréquence du sons émis par le diapason. 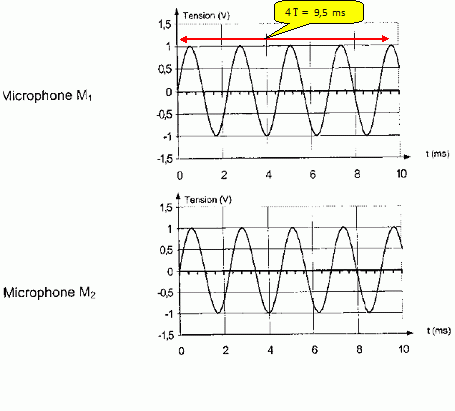T = 9,5 10-3 / 4 = 2,38 10-3 s ; f =1/T = 2,38 10-3= 4,2 102 Hz. JuLien éloigne le microphone M2 jusqu'à ce que les courbes soient de nouveau en phase. Il réitère l'opération jusqu' à compter cinq positions pour lesquelles les courbes sont à nouveau en phase. La distance D entre les deux microphones est alors D= 3,86 m    Pourquoi compte-t-on plusieurs retours en phase plutôt qu'un seul ? On améliore la précision sur le calcul de la longueur d'onde l. Définir la longueur d'onde et déduire sa valeur numérique de l'expérience précédente. La longueur d'onde l est la distance parcourue par le front de l'onde en une période, à la célérité c. D = 5 l ; l = D/5 = 3,86 / 5 = 0,772 m Calculer la célérité de l'onde. l = c = l / T = 0,772 /2,375 10-3 = 3,25 102 m/s. D'après les résultats expérimentaux obtenus, le milieu de propagation des ondes sonores est-il dispersif ? Les fréquences des sons ( diapason et coup de symbale ) sont différentes. Les ondes sonores se propagent pratiquement à la même célérité. Le milieu n'est donc pas dispersif ( la célérité ne dépend pas de la fréquence). Autre propriété des ondes sonores. Lors d'un concert donné par Julien dans une salle, des amis arrivés un peu en retard s'étonnent d'entendre de la musique alors qu'ils sont encore dans le hall et donc séparés de la scène par un mur très bien isolé phoniquement. Ils remarquent cependant que la porte, d'une largeur de 1,00 m, est ouverte. 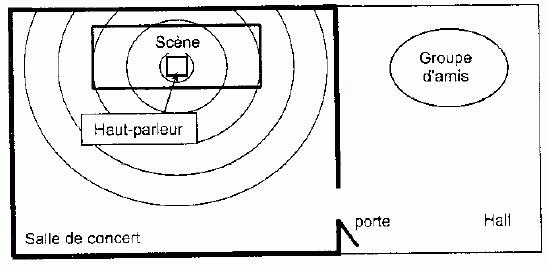La situation est représentée sur le schéma suivant : Quel phénomène physique permet d'explique l'observation faite par les amis de Julien ? La largeur de la porte est du même ordre de grandeur que la longueur d'onde des ondes sonores. L'ouverture provoque un phénomène de diffraction des ondes. Les amis de Julien ont-il entendu dans le hall des sons graves ( f = 100 Hz ) ou des sons très aigus ( f = 10 000 Hz) ? Justifier en calculant les longueurs d'ondes correspondantes. Sons graves : l = c / f = 3,3 102 / 100 = 3,3 m Sons très aigus : l = c / f = 3,3 102 / 10 000 = 0,033 m = 3,3 cm. La diffraction est importante pour les sons graves de longueur d'onde 3,3 m, valeur du même ordre de grandeur que la largeur de la porte. La diffraction est pratiquement nulle pour les sons très aigus : leur longueur d'onde est trop différente de la largeur de la porte. Les amis de Julien entendent des sons graves.

menu