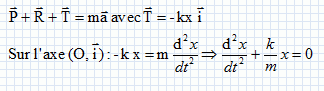L'oscillateur harmonique, mécanique quantique : bac S Liban 2010

l'oscillateur harmonique à une dimension est un modèle d'oscillateur qui intervient dans de nombreux domaines de la physique : mécanique, électricité notamment. Son évolution temporelle est régie par l'équation différentielle suivante : d2Y/dt2 + AY=0. Y est une grandeur physique qui varie au cours du temps, comme par exemple la position x d'un mobile ou la charge q d'un condensateur. A est une constante positive reliée à la période T0 de l'oscillateur par : A = 4 p2/T20. T0 est indépendante de l'amplitude de la grandeur Y. Le pendule simple. Un pendule simple a une longueur L égale à 100 cm. La période mesurée T est donnée dans le tableau suivant : amplitude (°) 0,00 5,00 10,00 15,00 20,00 25,00 30,00 35,00 période T (s) 2,01 2,01 2,01 2,02 2,03 2,04 2,05 On prendra g = 9,81 N / kg. La période propre T0 du pendule simple a pour expression T0 = 2 p ( L/g)½. Calculer sa valeur. T0 =6,28 ( 1,00 / 9,81)½=2,01 s. Pourquoi peut-on parler, d'après le tableau ci-dessus, d'isochronisme des petites oscillations ? Justifier. La période T mesurée est égale à T0 pour des angles inférieurs ou égaux à 15°. Dans le cas des petits angles, on peut confondre le sinus de l'angle et la mesure de l'angle en radian. Le pendule élastique. 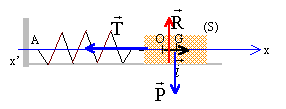Un solide S est relié à un ressort dont l'autre extrémité est fixe. Le solide de masse m = 205 g et de centre d'inertie G peut glisser sur un rail à coussin d'air horizontal. Le ressort, à spires non jointives, a une masse négligeable et une constante de raideur k = 10,0 N m-1. Au repos G est en O. A l'instant t, la position du solide est repérée par l'abscisse x(t) sur l'axe : x(t) représente également l'allongement du ressort. Un dispositif d'acquisition a permis d'obtenir l'enregistrement ci-dessous.   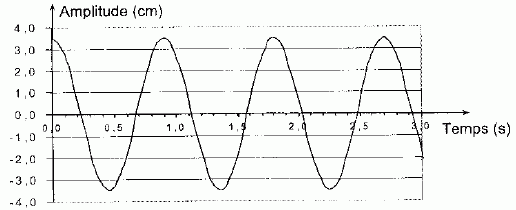Comment qualifier les oscillations obtenues ? Les oscillations sont sinusoïdales, non amorties ( l'amplitude est constante ). faire le bilan des forces s'exerçant sur S. Les représenter sans souci d'échelle. Le solide S est soumis à  : son poids, vertical, vers le bas, valeur mg - à l'action du rail, vertical, vers le haut, valeur mg - à une force de rappel exercée par le ressort, proportionnelle à l'allongement. Montre que dans ces conditions l'équation différentielle du mouvement s'écrit : d2x/dt2+k/m x = 0. 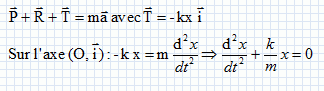Ecrire la seconde loi de Newton : Le pendule est assimilable à un oscillateur harmonique puisque l'équation ci-dessus est analogue à l'équation générale donnée au début de l'exercice. Déterminer l'expression de la période propre T0 en fonction de k et de m. A =k / m =  4 p2/T20 d'où T0 =2 p (m/k)½. A.N : T0 = 2 *3,14(0,205 / 10,0)½ =0,900 s. Déterminer la valeur expérimentale T0 exp en explicitant le raisonnement et la comparer avec la valeur calculée. 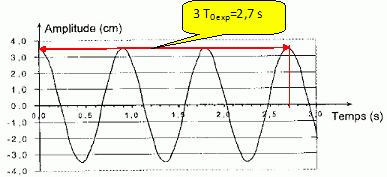T0 exp = T0 = 0,900 s. Energies. Comment appelle -t-on les énergies ayant respectivement pour expressions ½kx2 et ½m (dx/dt)2 ? Energie potentielle élastique : ½kx2 ; énergie cinétique : ½m(dx/dt)2. Pour un lâcher sans vitesse initiale, l'équation différentielle a pour solution x(t) = Xm cos (2p t / T0).   Montrer que l'énergie mécanique a pour expression EM =½kX2m. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. EM = ½k x2 + ½m(dx/dt)2 = ½kX2m cos2 (2p t / T0)+ ½m 4 p2/T02 X2m sin2 (2p t / T0) Or 4 p2/T02 = k/m d'où EM =½kX2m cos2 (2p t / T0)+½kX2m sin2 (2p t / T0) = ½kX2m. Quelle est la valeur minimale de l'énergie mécanique ? En absence de frottement, l'énergie mécanique se conserve. Xm = 3,5 cm = 0,035 m (lecture graphe). EM = 0,5*10,0 *0,0352 =6,1 10-3 J. On réalise différents lâchers sans vitesse initiale en faisant varier l'amplitude. Calculer l'énergie mécanique lorsque Xm = 1,00 cm ? EM = 0,5*10,0 *0,012 =5,00 10-4 J. Combien de valeurs de l'énergie mécanique sont possibles entre Xm=0 et Xm = 1,00 cm ? Aucune ou une infinité ? Justifier. Entre 0 et 1,00 cm, il y a une infinité de valeurs et toutes ces valeurs sont permises ( l'allongement  du ressort ( échelle humaine) , donc l'énergie ne sont pas quantifiés) ; l'énergie mécanique peut donc prendre une infinité de valeurs. Le pendule élastique en mécanique quantique. On considère une molécule diatomique AB vibrant autour de son centre d'inertie G ( mA et mB sont les masses respectives des atomes A et B ).. On assimile cette molécule à un système de masse µ oscillant par rapport au point G fixe. 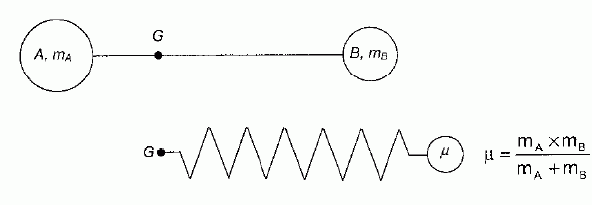Le mouvement est rectiligne sinusoïdal de période propre T0 = 2 p (µ / k)½ où k est la constante de raideur du ressort équivalent. On donne : h = 6,63 10-34 J s ; c = 3,00 108 m / s. La mécanique quantique montre que l'énergie de vibration Evib de la molécule est quantifiée. Qu'entend-on par énergie quantifiée ? Toutes les valeurs ne sont pas permises ; l'énergie  ne peut prendre qu'un petit nombre de valeurs. La molécule est assimilée à un oscillateur harmonique de période propre T0 = 1,95 10-14 s. Un niveau n d'énergie de vibration est caractérisé par Evib = (n+½)h v0, où h est la constante de Plank, v0 la fréquence de l'oscillateur et n un entier positif ( n=0, 1 2, ....) Vérifier que la fréquence v0 vaut environ 5,12 1013 Hz puis compléter le tableau suivant : v0 = 1/ T0 = 1 / 1,95 10-14 =5,13 1013 Hz. n 0 1 2 3 4 Evib ( x 10-20) J 8,50 11,90 15,30 Evib ( n=0) = 0,5 h v0 =0,5 *6,63 10-34 *5,13 1013 =1,70 10-20 J. Evib ( n=1) = 1,5 h v0 =1,5*6,63 10-34 *5,13 1013 =5,10 10-20 J. Représenter le diagramme en énergie de la molécule. Que peut-on dire de l'écart entre deux niveaux successifs ? 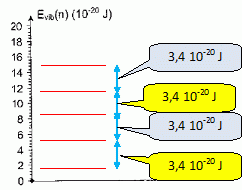La transition du niveau caractérisé par n= 0 au niveau caractérisé par n = 1 correspond à l'absorption d'une radiation. Calculer la longueur d'onde correspondante dans le vide. Cette radiation est-elle visible ? Justifier. DE = 3,4 10-20 J ; l = hc / DE = 6,63 10-34 * 3,00 108 / 3,40 10-20 = 5,85 10-6 m = 5,85 µm. Le domaine visible s'étend de 0,4 µm à 0,8 µm ; la radiation correspondante appartient à l'infrarouge.

menu