|
Lentille
convergente.
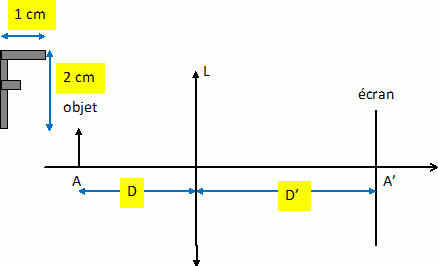
Sur
un banc d'optique de longueur 3,0 m on place une lentille mince
convergente L, un objet lumineux( une lettre F noire, placée sur un
papier translucide, de hauteur d = 2,0 cm ) , à la distance D de la
lentille.
On observe une image nette sur l'écran pour différentes valeurs de D.
Distance
focale et vergence.
D(m)
|
0,22
|
0,24
|
0,26
|
0,28
|
0,30
|
0,32
|
0,34
|
0,36
|
0,38
|
D'
(m)
|
0,99
|
0,72
|
0,59
|
0,50
|
0,45
|
0,41
|
0,38
|
0,36
|
0,34
|
x
= 1/D ( m-1)
|
4,55
|
4,17
|
3,85
|
3,57
|
3,33
|
3,13
|
2,94
|
2,78
|
2,63
|
| y
= 1/D' ( m-1) |
1,01
|
1,39
|
1,69
|
2,00
|
2,22
|
2,44
|
2,63
|
2,78
|
2,94
|
vergence
v = x+y ( m-1)
|
5,56
|
5,56
|
5,54
|
5,57
|
5,55
|
5,57
|
5,57
|
5,56
|
5,57
|
|
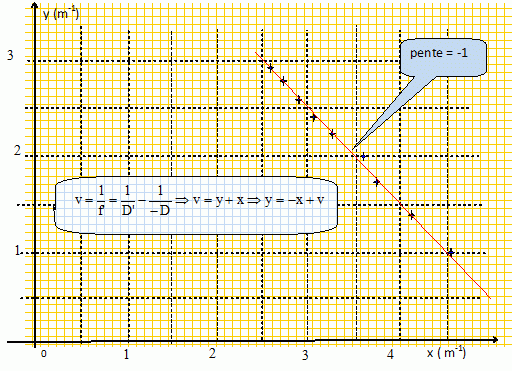
On trace la courbe y = f(x).
|
L'ordonnée
à l'origine donne la vergence v ~5,6 dioptries ; la distance focale
image f' est l'inverse de la vergence : f' = 1/5,6 ~0,18 m.
Taille
de l'image. ( Prendre D = D'
=0,36 m )
Le grandissement transversal g
( en valeur absolue) est égal = D'/D soit | g | = 1 dans ce cas.
L'image a alors la même taille que l'objet.
Dans le cas d'un écran carré de 16 cm de côté, on ne voit plus
entierement l'image si D est supérieure à :
| g | = 16/2 = 8 ; par suite D'/D =
8 ; D' = 8D.
De plus D+D' = 3 m d'où D = 3/9 = 0,33 m = 33 cm.
Quelle difficulté expérimentale
rencontre t-on :
- si D = 2,0 m , 1 / D' = v -1/D = 5,6-0,5 =5,1 ; D' =1/5,1 =0,196 ~0,2.
| g | =D'/D =0,2 / 2 = 0,1. La
taille de l'image est 2*0,1 = 0,2 cm = 2 mm ( l'image est pratiquement
réduite à un point).
- si D = 0,10 m, ( D <
f') : la lentille fonctionne en loupe et l'image ne peut pas être
obtenue sur un écran
Miroirs et lentille.
On considère un miroir sphérique convergent de distance focale f'
=-5,0 cm, de sommet F, de foyer F, de centre C.
Un objet AB de hauteur h = 2,0 cm, perpendiculaire à l'axe du miroir (
A est sur l'axe optique ), est tel que SA = 4SF.
Construction de
l'image A'B'.
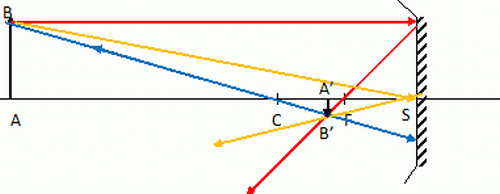
Tout rayon incident :
- passant par C se réfléchit sur lui
même
- passant par le sommet S donne un rayon
réfléchi symétrique du rayon incident
par rapport à l'axe optique CS.
- parallèle à CS donne un rayon
réfléchi passant par le foyer F.
Grandissement g :
L'image A'B'et l'objet AB sont de sens contraire : le grandissement est négatif.
Mesurer la hauteur de l'objet et la hauteur de l'image : l'image est à peu près trois fois plus petite que l'objet.
Le grandissement vaut donc : -1/3.
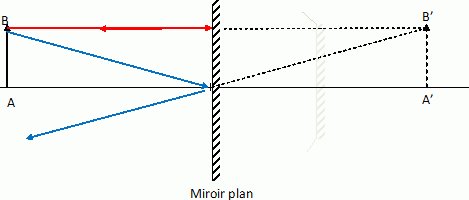
On
place un miroir plan, perpendiculaire à l'axe optique, au niveau du
point C. Ce miroir est suffisamment grand pour qu'aucun rayonlumineux
issu de l'objet AB ne parvienne sur le miroir sphérique. La face
réfléchissante est tournée vers l'objet.
L'image A'B', virtuelle, est symétrique de l'objet AB par rapport au plan du miroir. Le grandissement vaut 1.
|
A la place des deux miroirs, on place une lentille mince convergente de vergence C =5,0 dioptries.
Position de l'objet afin que le grandissement soit égal à -1/3.
La construction suivante positionne la lentille :
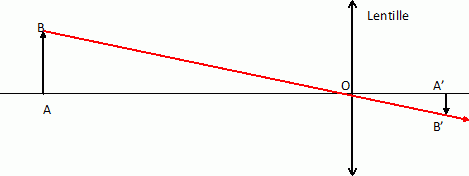
La construction suivante positionne les foyers :
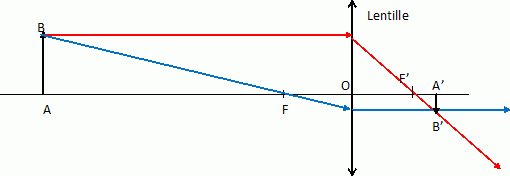
Où serait l'image si la lentille occupait la place du miroir sphérique précédent ?
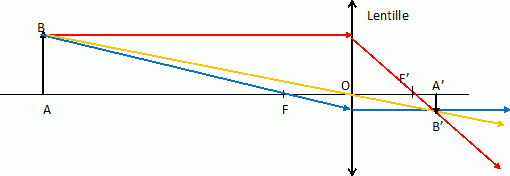
|
|






