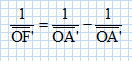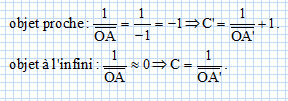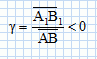Le dispositif d’Affichage Tête Haute
(ATH) est
principalement utilisé dans les
avions de chasse et certaines voitures. Il consiste à projeter des
informations
(valeur de la vitesse instantanée, indication sur la route à
suivre
...), devant le pare-brise d’un véhicule, dans le bas du champ de
vision
du conducteur. Ces images se superposent au paysage et permettent donc
au
conducteur de voir les informations fournies sans quitter la
route des yeux.

La
première partie de cet exercice montre l’intérêt
de ce dispositif d’affichage du point de vue de la sécurité et la
deuxième
partie en étudie le principe simplifié.
Intérêt
du dispositif ATH.
On étudie, au
préalable, la lecture de la vitesse affichée au compteur par un
conducteur dans
un véhicule qui n’est pas équipé du dispositif d’affichage ATH.
L’œil du conducteur
est modélisé par l’ensemble constitué de :
- une lentille mince
convergente, de centre O, de foyer image F’œil et de
distance focale
f ’œil réglable, qui représente
le système optique convergent de l’œil ;
- un écran plat
vertical représentant la rétine, sur laquelle se forme l’image.
L’orbite de l’œil
n’étant
pas déformable, la distance entre l’écran et la lentille est fixe.
On rappelle qu’un œil
normal au repos voit net un objet situé à l’infini.
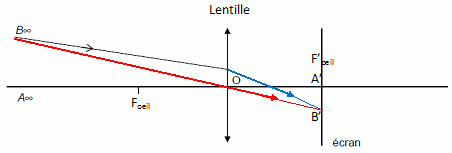
Le conducteur
voit net un objet AB situé à l’infini.
Sur la figure tracer
l’image A’B’
de l’objet AB situé à l’infini.
Indiquer,
sur
la figure, les
positions du foyer objet Fœil et du foyer
image F’œil de la lentille
modélisant l’œil du conducteur.
L'image d'un objet à l'infini se forme dans la plan focal image.
L'image nette se forme sur la rétine.
L’expression de
la relation de conjugaison pour une lentille mince est :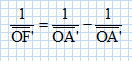
|
Que représentent les
distances OA, OA’ et OF’ ?
OA : distance lentille-objet ; OA' : distance lentille-image ; OF' :
distance focale image.
Définir la
vergence C d’une lentille en
indiquant son unité.
La vergence est l'inverse de la distance focale image exprimée en
mètre. La vergence s'exprime en dioptries ( d).
|
Pour contrôler
sa vitesse, le conducteur regarde maintenant le compteur de vitesse
situé à une
distance d’environ un mètre de son œil.
La valeur de la
vergence de la lentille qui modélise l’œil doit-elle augmenter ou
diminuer par
rapport à sa valeur au repos pour voir nettement le compteur de vitesse
?
Justifier.
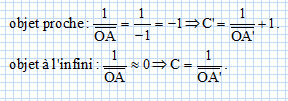
OA' est constante, l'image nette se forme sur la rétine : C' > C ;
la vergence de l'oeil croït.
. La notice d’utilisation
d’un afficheur tête haute du commerce donne les informations suivantes :
« En disposant d’informations
dans son champ de vision, le conducteur évite ainsi des allers et des
retours
du regard entre le tableau de bord et la route. L’effet d’éloignement
des
images projetées lui évite également de réadapter constamment sa vue à
des
changements de distance. Dispensé de ces deux actions, le conducteur
gagne
alors environ une seconde d’attention
... »
D’après
la notice d’utilisation d’un afficheur tête haute du commerce
Quelle
distance parcourt une voiture roulant à la vitesse de 120 km/h pendant
la « seconde
d’attention » perdue lors d’un
aller-retour du regard ?
d
= v t avec v = 120 /3,6 ~33 m/s et t = 1s ; d ~33 m.
En déduire l’intérêt
principal de l’affichage tête
haute.
Le conducteur évite des
allers et des retours
du regard entre le tableau de bord et la route ; il évite également de réadapter constamment
sa vue à des
changements de distance.
Le conducteur sera donc plus attentif à ce qui se passe sur la route.
Principe de
l'affichage tête haute.
La technologie embarquée sur les
automobiles actuelles fonctionne avec un dispositif optique situé
derrière le
tableau de bord qui projette des informations au-delà du pare-brise, le
conducteur ayant l’illusion que ces dernières se trouvent à l’extérieur
de la voiture, à environ 1
mètre par rapport au bas du pare-brise.
Principe de l’affichage tête haute, d’après un site
Internet
L’ensemble
du
dispositif optique installé dans le tableau de bord est constitué :
-
d’une
source lumineuse à diodes affichant la valeur de la vitesse, considérée
dans l’exercice
comme l’objet lumineux AB ;
-
d’une
lentille mince convergente de distance focale f ’.
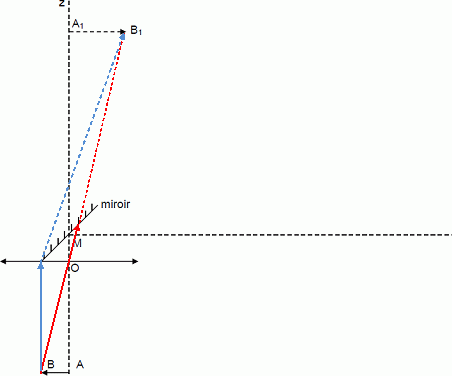
Sur la figure 3 de l'annexe schématisant le
dispositif, on a représenté l’image A1B1, de
l’objet AB
donnée par la lentille.
Tracer la marche
de deux rayons issus de B permettant de construire l’image B1.
Définir le
grandissement g
de la lentille. Sa valeur algébrique est-elle positive ou négative ? Sa
valeur
absolue est-elle supérieure ou inférieure à 1 ?
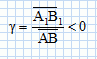
La valeur algébrique du grandissement
est négative, car l'objet et l'image sont de sens contraire.
L'image est plus grande que l'objet : la valeur absolue du
grandissement est supérieure à 1.
|
Réflexion
sur le
pare-brise.
L’image A1B1 de
la partie
précédente est ensuite réfléchie vers le pare-brise. Pour simplifier le
problème, on peut considérer que le pare-brise se comporte pour A1B1
comme un miroir plan, incliné de 45° par rapport à la verticale Oz.
Quel
rôle joue A1B1
pour le miroir plan ?
A1B1
joue le rôle d'objet pour le miroir plan.
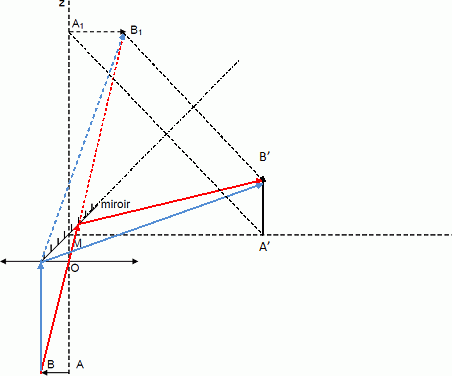
Sur la figure,
placer l’image A’B’
de A1B1, donnée par le miroir plan. Justifier.
L'image A'B' et l'objet A1B1 sont symétriques par rapport au plan du
miroir.
On voudrait
faire en sorte que les indications de l’affichage tête haute soient
plus
grandes. Sans faire de calcul, quelle solution proposeriez-vous ?
Diminuer la distance objet-lentille; cette
distance doit rester supérieure à la distance focale de la lentille,
sinon celle-ci fonctionnerait en loupe.
|