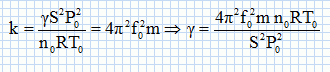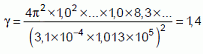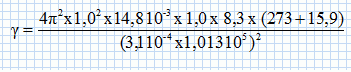L’une des expériences historiques
permettant de déterminer la célérité du son dans l’air a été réalisée en 1822
près de Paris par ordre du Bureau des Longitudes. Présenté ci-dessous,
l’extrait du traité élémentaire de physique (1836) de Monsieur l’abbé Pinault
relate cette expérience.
Les deux stations que l’on avait
choisies étaient Villejuif et Montlhéry. À Villejuif, le capitaine Boscary fit
déposer, sur un point élevé, une pièce de six1, avec des gargousses2
de deux et trois livres de poudre.
À Montlhéry, le capitaine Pernetty fit
déposer une pièce de même calibre, avec des gargousses de même poids. Les
expériences furent faites de nuit et commencèrent à onze heures du soir, le 21
et le 22 juin 1822. De Villejuif on apercevait très distinctement le feu de
l’explosion de Montlhéry et vice
versa : le ciel était serein et à peu près calme.
La température de l’atmosphère était de
15,9 degrés Celsius. Les coups de canon des deux stations opposées étaient
réciproques, de sorte que les résultats ne fussent pas influencés par le vent.
Chacun des observateurs notait sur son
chronomètre le temps moyen ( Dt = 54,6 s ) que le son mettait à passer d’une station à l’autre.
Les deux canons étaient à une distance de 9 549,6 toises3.
1 pièce de canon ;2 charge de poudre contenue dans une enveloppe de tissu ou
de papier au diamètre de la chambre du canon.3 unité de longueur ancienne qui correspond à 1,949 m.
Données :
- célérité de la
lumière dans l’air c = 3,0 ×108 m.s-1 ;constante des gaz
parfaits R = 8,3 J.K-1.mol-1 ; masse d’une mole
d’air M = 2,9 ×10-2
kg.mol-1 ; température
absolue T(K) = q(°C)
+ 273,1.
Détermination expérimentale et historique de la
célérité des ondes sonores dans l’air.
Les ondes
sonores sont des ondes mécaniques longitudinales.
Définir une onde mécanique
puis préciser ce que signifie le caractère longitudinal de l’onde sonore.
On appelle onde mécanique progressive le phénomène de propagation d'une
perturbation dans un milieu matériel sans transport de matière, mais avec
transport d'énergie.
Une onde se propage, à partir de la source, dans toutes les directions qui
lui sont offertes.
Une onde est longitudinale lorsque le déplacement des points du milieu de
propagation s'effectue dans la même direction que celle de la propagation.
L'onde sonore se propage dans les trois dimensions de l'espace. Chaque
point P vibre longitudinalement dans la direction de
propagation du signal.
Dans
l’expérience, la célérité des ondes sonores produites par les deux canons
opposées est-elle augmentée, diminuée ou inchangée lors de leur
croisement ?
Lors du croisement les ondes se superposent ; leur célérité est inchangée.
En utilisant
les valeurs mesurées par les observateurs, calculer la valeur de la célérité
des ondes sonores, notée vexp.
D’après le texte, pour les observateurs, de quel(s) paramètres(s) dépend, a
priori, la célérité du son ?
Les deux canons étaient à une distance de 9 549,6 toises soit : d = 9 549,6*1,949 =18612.
vex = d / Dt =18612 / 54,6 = 341 m s-1.
Cette célérité dépend de la température, d'après les observateurs.
Les
observateurs déclenchent leur chronomètre à l’apparition de la lumière.
Quelle
durée négligent-t-ils ? Pourquoi est-ce
raisonnable ?
Ils négligent la
durée mise par la lumière pour parcourir la distance d = 18,6 km. Cela
est raisonable car la célérité de la lumière est environ 106 fois plus grande que celle du son.
|
Détermination de la célérité des ondes sonores dans l’air en utilisant un modèle théorique.
Le développement de la mécanique des fluides a permis d’élaborer un
modèle pour la propagation des ondes mécaniques dans les gaz.
L’expression théorique de la célérité de ces ondes qui découle de ce
modèle est : vthéo = [gRT / M]½.
Avec M la masse d’une mole d’air, T sa température absolue, R la constante des gaz parfaits et g un
nombre sans dimension qui dépend notamment des propriétés de l’air.
|
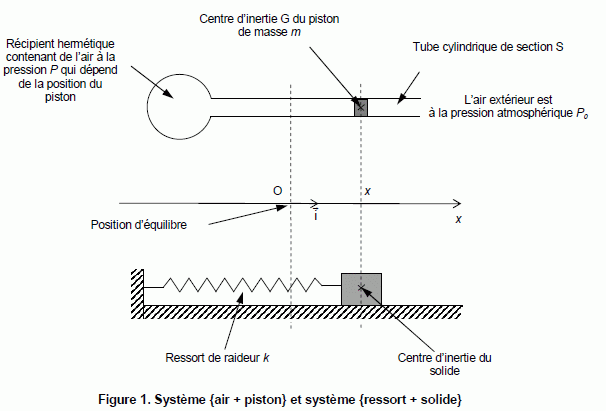
La valeur du coefficient g
de l’air a été déterminée par Rückhardt (1929, scientifique allemand)
en utilisant les propriétés élastiques des gaz avec le dispositif
schématisé ci-dessous :
 .
.
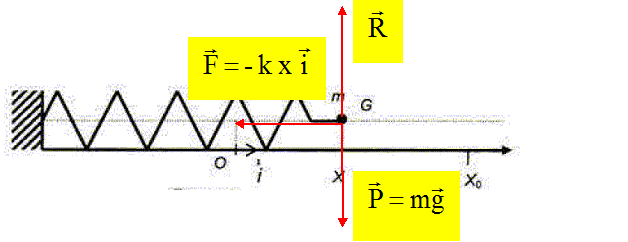
Un piston étanche coulisse sans frottement dans un tube cylindrique ;
le tube et le récipient enferment une quantité de matière n0 d’air. Le piston écarté de sa position d’équilibre oscille autour de cette position d’un
mouvement analogue à celui de l’oscillateur élastique {ressort + solide de masse m}.
Le système {air + piston de masse m} est équivalent à un système {ressort + solide de masse m}.
Le référentiel
d’étude est le référentiel terrestre considéré comme galiléen.
La position du
piston est repérée par son abscisse x
sur l’axe Ox dont l’origine O est
confondue avec la position du piston à l’équilibre.
Dans tout l’exercice, les frottements sont négligés.
L’air extérieur et l’air intérieur sont à la même température. Cette
température est constante tout au long de l’expérience, on la note T0.
Le piston est
soumis aux forces citées ci-dessous :
- Le poids ; la réaction du support ;
les forces pressantes de l’air à
l’intérieur du récipient, dont la somme est équivalente à une force unique ; les forces pressantes de l’air à
l’extérieur du récipient, dont la somme est équivalente à une force unique.
Donner pour chacune
de ces forces la nature de l’interaction : interaction de contact ou à
distance.
Le poids est une
interaction s'exerçant à distance ; la réaction du support et les
forces pressantes sont des interactions de contact.
L’ensemble des
forces s’exerçant sur le piston est équivalent à une force unique
horizontale :
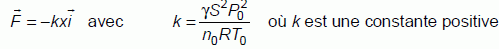
Pourquoi
peut-on dire que cette force se comporte comme une force de rappel ?
Justifier.
Le vecteur force et le vecteur unitaire de l'axe sont toujours de sens contraire.
La force F est toujours dirigée vers la position d'équilibre O (
ressort non déformé ). Cette force a tendance à ramener (
rappeler ) le centre de gravité G de la masse fixée au ressort vers le
point O.
Énoncer la deuxième loi de Newton.
Dans un référentiel
galiléen, la somme vectorielle des forces extérieures appliquées à un solide est
égale au produit de la masse M du solide par l'accélération de son centre
d'inertie.
Déterminer l’équation
différentielle du mouvement du centre d’inertie G du piston, en projetant sur
l’axe (Ox) l’égalité vectorielle
obtenue en appliquant la deuxième loi de Newton.
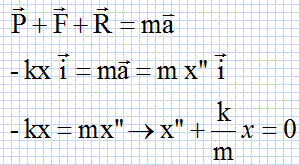
L’équation différentielle obtenue peut s’écrire sous la forme : x" + 4p2f02 x = 0.
En déduire l’expression de k en fonction de la masse m du piston et de sa fréquence propre f0.
Par identification k / m = 4p2f02 ; k = 4p2f02 m.
Montrer que le
coefficient g
a pour expression : 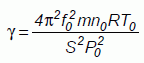 .
.
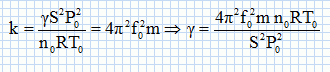
|
Dans les unités du
système international, on trouve g
= 1,4 à la température q
= 15,9 °C de l’atmosphère dans la nuit du 21 juin 1822.
Recopier et
compléter le calcul qu’il faut poser pour obtenir ce résultat.
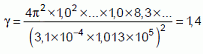
Données :
masse du piston : m = 14,8 g ; section du tube cylindrique S = 3,1 cm2 ; fréquence propre f0 = 1,0 Hz ;
pression atmosphérique P0 =1,013 bar ; 1 bar = 105 Pa ; n0 = 1,0 mol.
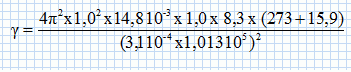
Calculer la
valeur théorique vthéo de
la célérité des ondes sonores dans l’air à cette température q.
vthéo = [gRT / M]½ = [1,4 *8,3 *(273+15,9) / 2,9 10-2]½ =3,4 102 m/s.
Cohérence avec la mesure effectuée dans la nuit du 21
juin 1822 .
Vérifier que
la valeur théorique vthéo
est proche de la valeur expérimentale vexp.
Ecart relatif : (341-340) / 341 ~3 10-3 ou 0,3 %.
L'écart relatif est très faible, les valeurs théorique et expérimentale sont très proches.
Si
l’expérience s’était déroulée en hiver avec une température extérieure de 0°C
et en considérant que g reste constant, la valeur trouvée de la
célérité serait-elle plus grande ou plus petite ? Justifier.
vthéo = [gRT / M]½ ;
la vitesse est proportionnelle à la racine carrée de la température absolue : si la température diminue, la vitesse diminue.
|
 .
.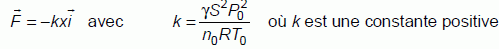

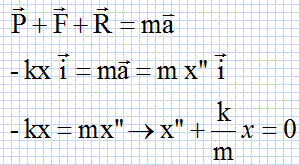
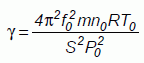 .
.