Nucléaire au service de la médecine : bac S France 2010

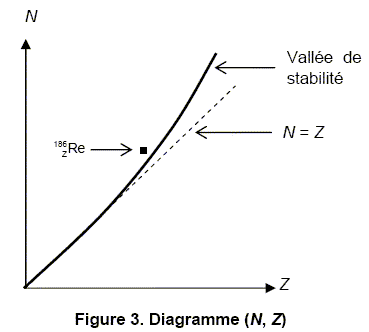
La médecine nucléaire désigne l’ensemble des applications où des substances radioactives sont associées au diagnostic et à la thérapie. Depuis les années 1930, la médecine nucléaire progresse grâce à la découverte et à la maîtrise de nouveaux isotopes. La radiothérapie vise à administrer un radiopharmaceutique dont les rayonnements ionisants sont destinés à traiter un organe cible dans un but curatif ou palliatif. Ainsi on utilise du rhénium 186 dans le but de soulager la maladie rhumatoïde et du phosphore 32 pour réduire la production excessive de globules rouges dans la moelle osseuse. D’après le site : http://www.asn.fr La première partie de cet exercice traite de l’utilisation du rhénium 186 et la seconde partie de l’utilisation du phosphore 32. On s’intéresse à l'aspect physique des phénomènes, les aspects biologiques ne sont pas pris en compte. Données : - temps de demi-vie du rhénium 186 : t½( 186ZRe) = 3,7 j (jours) ;  constantes radioactives : λ( 186ZRe) = 2,2 × 10−6 s− 1 ; λ( 3215P) = 5,6 × 10−7 s− 1 ; - masse molaire du rhénium 186 : M( 186ZRe) =186 g/mol ; - masses de quelques noyaux et particules : m( 3215P) = 5,30803 × 10−26 kg ; m( 3216S ) = 5,30763 × 10−26 kg ; m( 0-1e ) = 9,1 × 10−31 kg ; - célérité de la lumière dans le vide : c = 3,0 × 108 m.s− 1 ; - constante d'Avogadro : NA = 6,0 × 1023 mol− 1 ; électron-volt : 1 eV = 1,6 × 10−19 J . Le rhénium 186 ( 186ZRe ) est un noyau radioactif β−. Sur le diagramme (N, Z) de la figure 3 ci-dessous où N représente le nombre de neutrons et Z le nombre de protons, la courbe tracée permet de situer la vallée de stabilité des isotopes. Le point représentatif du noyau de rhénium 186 est placé au-dessus de cette courbe. Déduire de ce diagramme si cet isotope radioactif possède un excès de neutron(s) ou un excès de proton(s) par rapport à un isotope stable du même élément. Le rhénium 186 est situé à gauche de la vallée de la stabilité : il possède un excès de neutrons par rapport à un isotope stable du même élément.  Quel nom porte la particule émise au cours d’une désintégration β− ? Electron. Écrire l’équation de la désintégration du noyau de rhénium 186 noté ( 186ZRe) sachant que le noyau fils obtenu correspond à un isotope de l'osmium noté ( A76Os ). En énonçant les lois utilisées, déterminer les valeurs de A et de Z. On admet que le noyau fils obtenu lors de cette transformation n’est pas dans un état excité. 186ZRe ---> A76Os + 0-1e. Conservation de la charge : Z =76 -1 d'où Z =75. Conservation  du nombre de nucléons : 186 = A +0. 18675Re ---> 18676Os + 0-1e. Le produit injectable se présente sous la forme d’une solution contenue dans un flacon de volume Vflacon = 10 mL ayant une activité A0 = 3700 MBq à la date de calibration, c'est-à-dire à la sortie du laboratoire pharmaceutique. Pourquoi est-il précisé "à la date de calibration" en plus de l’activité ? La demi-vie radioactive du rhénium 186 est de 3,7 jours. L'activité  au bout de 3,7 j est donc déja divisée par 2. Calcul du volume de la solution à injecter. L’activité A(t) d’un échantillon radioactif peut s’exprimer par la relation suivante A(t) = λ.N(t) où N(t) représente le nombre de noyaux radioactifs à la date t et λ la constante radioactive.  Calculer la masse m de rhénium 186 contenu dans le flacon de volume Vflacon à la date de calibration. N0 = A0 / l = 3700 106 / 2,2 × 10−6  = 1,68 1015 ~ 1,7 1015 noyaux. n = 1,68 1015 / NA = 1,68 1015 / 6,0 × 1023 =2,80 10-9 mol masse = n M = 2,80 10-9 *186 = 5,2 10-7 g.  En s’aidant des données, quelle est la valeur de l’activité A1 de l’échantillon contenu dans le flacon au bout de 3,7 jours après la date de calibration ? L'activité initiale est divisée par deux au bout d'une demi-vie ( 3,7 j) : A1 = 3700 / 2 = 1,85 103 MBq. L’activité de l’échantillon à injecter dans l’articulation d’une épaule est Athérapie = 70 MBq. En supposant que l’injection a lieu 3,7 jours après la date de calibration, calculer le volume V de la solution à injecter dans l’épaule. 1850 MBq dans 10 mL ; 70 MBq  dans V = 10*70/1850 = 0,38 mL. Injection intraveineuse d'une solution contenant du phosphore 32. Carte d’identité du phosphore 32 : 3215P ; type de radioactivité ß- ; énergie du rayonnement émis : 1,7 MeV équation de désintégration : 3215P ---> 3216S + 0-1e ; demi-vie t½ = 14 j. L’injection en voie veineuse d’une solution contenant du phosphore 32 radioactif permet dans certains cas de traiter une production excessive de globules rouges au niveau des cellules de la moelle osseuse. Donner la composition du noyau de phosphore 32. 15 protons et 32-15 = 17 neutrons.  À l’aide des masses données en début d’exercice et de la carte d’identité du phosphore 32, vérifier par un calcul la valeur E de l'énergie du rayonnement émis par la désintégration du phosphore 32. Défaut de masse : Dm = m( 3216S ) +m( 0-1e ) -m( 3215P) = 5,30763 × 10−26 +9,1 × 10−31 - 5,30803 × 10−26 = -3,09 10-30 kg. E = |Dm|c2 =3,09 10-30 * (3,0 × 108)2 = 2,78 10-13 J 2,78 10-13 / 1,6 × 10−19 =1,7 106 eV = 1,7 meV. Pour la très grande majorité d’entre eux, les noyaux fils obtenus lors de cette transformation ne sont pas dans un état excité.  À quel type de rayonnement particulièrement pénétrant le patient n'est-il pas exposé ? Un noyau excité libère son surplus d'énergie en émettant des photons g. Rappeler la loi de décroissance du nombre N(t) de noyaux radioactifs d’un échantillon en fonction de λet N0 (nombre de noyaux radioactifs à la date t = 0). Définir le temps de demi-vie radioactive t½ et établir la relation qui existe entre la demi-vie et la constante de désintégration radioactive λ. N(t½) = 0,5 N0 = N0 exp(-l t½) ;  0,5 = exp(-l t½) ; ln 0,5 = - ln 2 = -l t½ ; l t½  = ln 2. Vérifier, par un calcul, la valeur approchée du temps de demi-vie proposée dans la carte d’identité cidessus. t½  = ln 2 / l = ln 2 / 5,6 × 10−7  = 1,24 106 s ou 1,24 106 / 3600 ~344 heures ou 344 / 24 ~14 jours.

menu