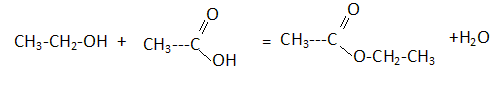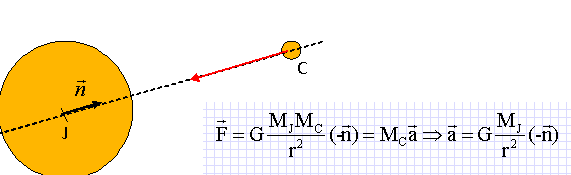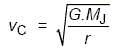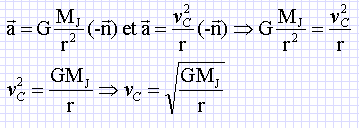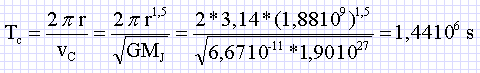Dans cette partie, on
étudie la transformation chimique entre l'acide éthanoïque et l'éthanol
afin de comprendre la phrase notée en gras dans le texte.
On donne :
| acide éthanoïque | éthanol | éthanoate d'éthyle |
| masse molaire ( g/mol) | 60,0 | 46,0 | 88,0 |
| masse volumique r ( g/mL) | 1,05 | 0,79 | 0,90 |
Au laboratoire, on mélange dans un flacon, un volume V1 = 57 mL d'acide éthanoïque et un volume V2 = 58 mL d'éthanol. Le flacon est ensuite hermétiquement fermé et placé dans l'obscurité à température ambiante. On laisse le système évoluer pendant six mois ; après cette durée, l'état final du système n''est pas encore atteint.
Déterminer la quantité de matière initiale n1 d'acide éthanoïque et montrer que le mélange est équimolaire.
n1 = V1 r / M = 57*1,05 / 60,0 = 0,9975 ~1,0 mol.
éthanol : 58*0,79 / 46 = 0,996 ~1,0 mol.
|
Etude du milieu réactionnel au bout de six mois.
Au
bout de six mois, le flacon est ouvert et on y prélève un volume V =
2,0 mL du mélange. L'acide éthanoïque restant dans ce prélèvement est
dosé, à froid, à l’aide d’une solution d’hydroxyde de sodium de
concentration CB = 1,00 mol.L-1 en présence de phénolphtaléine comme indicateur coloré de fin de dosage.
Le volume équivalent est égal à VE = 12,0 mL.
|
À
l’aide des formules semi-développées, écrire l’équation de l’équilibre
chimique d’estérification entre l’acide éthanoïque et l’éthanol.
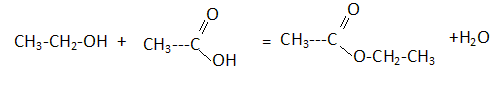
Écrire l’équation de la réaction chimique support du dosage.
HO-aq + CH3COOH aq = CH3COO-aq + H2O(l).
Définir l'équivalence du dosage et en déduire la quantité de matière nR d’acide éthanoïque restant au bout de six mois dans le prélèvement de 2,0 mL.
A
l'équivalence les quantités de matière des réactifs mis en présence
sont en propotions stoechiométriques. Avant l'équivalence l'un des
réactifs est en excès, après l'équivalence, l'autre réactif est en
excès.
nR = VE CB = 12,0 10-3 * 1,00 = 1,20 10-2 mol.
En supposant que le volume du milieu réactionnel est resté constant au cours du temps, en déduire la quantité de matière nR’ d’acide éthanoïque restant au bout de six mois dans le milieu
réactionnel.
Volume total du mélange réactionnel : 57+58 = 115 mL
nR’ =1,20 10-2 *115 / 2 =0,69 mol.
Déterminer les quantités de matière de toutes les espèces chimiques présentes dans le flacon au bout de six mois. On peut s'aider éventuellement d’un tableau d’avancement.
Acide éthanoïque ayant réagi : 1,0-0,69 =0,31 mol.
0,31 mol d'acide éthanoïque réagit avec 0,31 mol d'alcool en donnant 0,31 mol d'ester et 0,31 mol d'eau.
Acide éhtanoïque : 0,69 mol ; éthanol : 0,69 mol ; ester : 0,31 mol ; eau : 0,31 mol.
À
partir des résultats obtenus à la question précédente, justifier la
phrase en gras dans le texte de Berthelot et Péan de Saint Gilles. Aucun calcul n’est demandé.
Connaissant
les quantités de matières initiales et la quantité de matière finale de
l'acide éthanoïque, sachant de plus qu'une mole d'acide réagit avec une
mole d'alcol pour donner une mole d'ester et une mole d'eau, les
quantités de matière de toutes les espèces peuventt être connues à
chaque instant.

Dans cette partie, on étudie le mouvement du satellite Callisto par rapport à la planète Jupiter.
Données :
- constante de gravitation universelle : G = 6,67 × 10−11 m3.kg−1.s−2 ;
-
la planète Jupiter de centre J et son satellite Callisto de centre C
sont des astres que l’on considère à répartition de masse à symétrie
sphérique ;
- la masse de Jupiter est égale à MJ = 1,90 × 1027 kg et celle de Callisto est notée MC ;
- Callisto décrit autour de Jupiter une orbite circulaire de rayon r = 1,88 × 106 km.
Le mouvement de Callisto est étudié dans le référentiel galiléen lié au centre de Jupiter, appelé référentiel jovicentrique.
Sans
souci d’échelle, représenter sur un schéma la force F exercée par
Jupiter sur le satellite Callisto en orbite circulaire autour de Jupiter.
En utilisant les notations de l’énoncé, donner l’expression vectorielle de cette force.
En appliquant la seconde loi de Newton à Callisto, déterminer l’expression du vecteur accélération de son centre C.
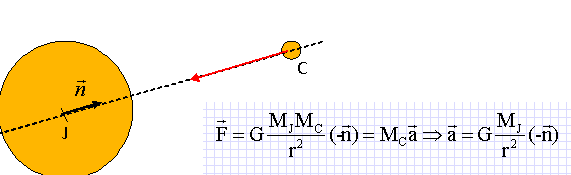
À propos des forces, donner la signification de chacune des deux parties de phrase en gras à la fin du texte de Newton.
"Les
forces tendent au centre de Jupiter " : la force exercée par Jupiter
sur Callisto est dirigée constamment vers le centre de Jupiter ( force
centripète ).
" sont en raison réciproque des carrés de leurs
distance à ce centre": les forces de gravitation sont inversement
proportionnelles au carré de la distance qui sépare les centres des
astres à symétrie sphérique.
On considère que le mouvement de Callisto est uniforme sur son orbite. On note vC la vitesse du centre C du satellite Callisto.
Donner l’expression de l’accélération aC du centre C de Callisto en fonction de vC et r.
Montrer que la vitesse vC peut s’exprimer par :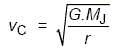
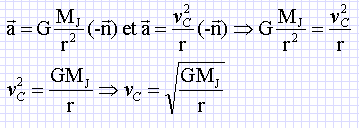
Étude de la période de révolution du satellite Callisto autour de Jupiter
Déterminer l’expression de la période de révolution TC du satellite Callisto autour de Jupiter en fonction de G, MJ et r.
Calculer la valeur de cette période.
La circonférence 2 p r est parcourue à la vitesse vC en une durée TC : 2 p r = vC TC ;
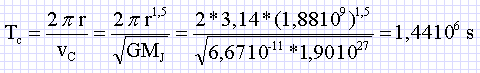
|
Étude de la période de révolution du satellite Callisto autour de Jupiter.
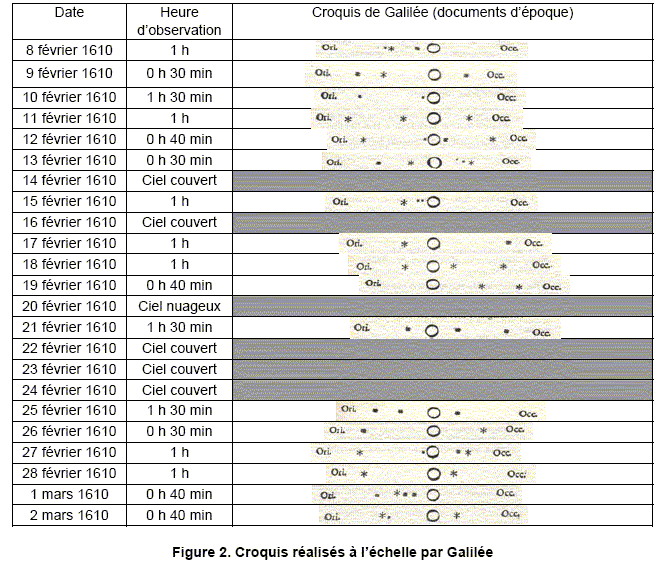
La figure 2 donne les croquis réalisés à l’échelle par Galilée entre le 8 février 1610 et le 2 mars 1610.
3.2.1. À certaines dates, le satellite Callisto apparaît le plus éloigné de Jupiter pour Galilée. À l’aide de
la figure 1, justifier cette observation.
3.2.2. On cherche à déterminer la valeur approchée de la période TC de révolution de Callisto autour de
Jupiter. Le 11 février, Callisto apparaît pour Galilée comme étant le plus éloigné à l’Est (« Ori. »)
de Jupiter.
a. À quelle date, Galilée voit-il Callisto à nouveau le plus éloigné à l’Est de Jupiter ?
b. En déduire la valeur approchée de la période TC. Un résultat en nombre de jours entier est
attendu. Est-ce compatible avec le résultat obtenu au 2.7.2 ?
Par rapport à Jupiter, les orbites des satellites sont pratiquement circulaires et appartiennent quasiment au
même
plan (P) qui est celui de l'équateur de Jupiter. Les orbites sont
représentées. Les positions des satellites sont indiquées à une date
donnée. Le schéma a été réalisé sans souci d’échelle.
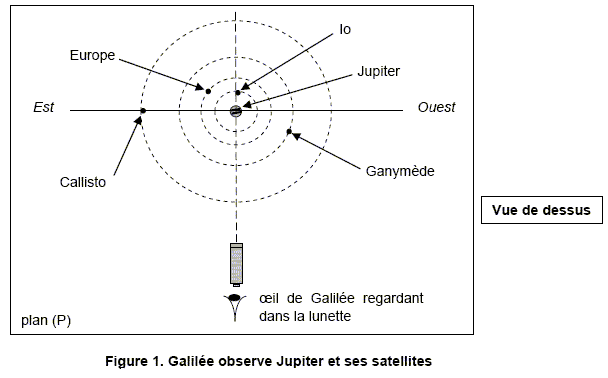
On admet que Galilée, regardant dans sa lunette depuis un point de la Terre, appartient au plan (P) défini précédemment.
La figure correspond-elle au croquis (a), (b) ou (c) ci-dessus ? Justifier.
Le schéma a convient : Calisto et Europe sont à l'est ; Ganymède est à l'ouest et Io est masqué par Jupiter.
Donner
une raison possible permettant d’expliquer pourquoi les quatre
satellites ne sont pas toujours vus en même temps par Galilée.
L'un des satellites peut être masqué par Jupiter.
Quelle est la trajectoire des satellites de Jupiter vue par Galilée ?
" de petits astres tournant autour de Jupiter comme la Lune tourne autour de la Terre."
Trajectoire circulaire.
|