L'observatoire du Harvard College aux
Etats Unis, s'est doté en 1847 d'une lunette dont l'objectif a un
diamètre de 38 cm. Il s'agissait d'un instrument rmarquable pour
l'époque au point de rester célèbre sous le nom de "Grand réfracteur ".
Cet instrument a permis de réaliser la première photographie d'une
étoile en 1850 : l'astronome W. C. Bond a réalisé des daguerréotypes de
l'étoile Véga dans la constellation de la Lyre. D'après Astronomie aux
éditions Atlas.
Située près de la constellation de la Lyre, la nébuleuse annulaire de
la Lyre ( nommée M57 ) est le prototype des nébuleuses planétaires.
Elle s'est formée il y a environ 20 000 ans à partir d'une étoile qui,
en explosant, a libérée dea gaz ayant une structure que l'on assimilera
a un anneau circulaire. L'exercice propose de déterminer le diamètre
apparent de cette nébuleuse que l'on désignera par M 57 dans le texte,
observée avec une lunette de l'observatoire de Harvard. Pour cela, on
négligera le phénomène de diffraction qui intervient dans l'utilisation
d'une lunette. On rappelle qu'une lunette est dite afocale lorsque le
foyer image de l'objectif et le foyer objet de l'oculaire sont
confondus.
Pour les
angles petits exprimés en radians : tan a ~ a.
On prendra comme valeur de l'année lumière : 1 a. l = 1,00 1013
km.
La lunette sera
modélisée par un système de deux lentilles minces L1 et L2.
L'objectif L1 est une lentille convergente de centre optique
O1, de diamètre 38,0 cm et de distance focale f'1
= 6,80 m.
L'oculaire L2
est une lentille convergente de centre optique O2, de
diamètre 38,0 cm et de distance focale f'2 = 4,0 cm. La
distance entre les centres optiques des deux lentilles est de 6,84 cm.
|
Montrer que cette
lunette est afocale.
On note F'1 le foyer image de l'objectif et F2 le
foyer objet de l'oculaire.
O1O2 = O1F'1 +F'1F2
+F2O2.
F'1F2
= O1O2
-O1F'1
-F2O2
= 6,84 -6,80-0,04 = 0.
F'1 et F2 sont
confondus : la lunette est afocale. |
La nébuleuse, supposée à l'infini, est représentée par AooBoo.
Sur un schéma,
réalisé sans soucis d'échelle, placer les deux lentilles, le foyer
image F'1
de L1, les foyers F2 et F'2 de l'oculaire.
Construire
sur le schéma, l'image A1B1 de l'objet AooBoo, donné par
l'objectif
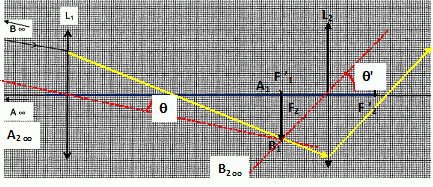
On désigne
par q le diamètre apparent
de la nébuleuse M 57, q est
l'angle sous lequel on voit l'objet à l'oeil nu.
Quel est en fonction de f'1 et A1B1, l'expression du diamètre apparent q ?
tan q = A1B1 / f'1
~ q ( exprimé en radian ) si l'angle est petit.
L'oculaire L2 permet d'obtenir une image définitive A'B' de la nébuleuse M 57.
La lunette étant afocale, où sera située l'image A'B' ? Justifier.
A1B1 joue le rôle d'objet pour l'oculaire. L'objet A1B1 est situé au foyer objet de L2 : l'image définitive est donc à l'infini, notée A2ooB2oo sur le schéma ci-dessus.
Construire la marche d'un rayon lumineux issu de B1 permettant de trouver la direction de B'.
Voir schéma ci-dessus.
On désigne par q' le diamètre apparent de l'image A'B' vue à travers la lunette, q' est l'angle sopus lequel on voit l'image donnée par l'instrument.
Quel est en fonction de f'2 et A1B1, l'expression du diamètre apparent q' ?
tan q' = A1B1 / f'2
~ q' ( exprimé en radian ) si l'angle est petit.
On appelle grossissement G d'un instrument d'optique le rapport G = q' q.
Donner l'expression de G puis calculer sa valeur.
tan q =A1B1 / f'1 ~q ; tan q' =A1B1 / f'2 ~q'
G = q' / q =f'1 / f'2 =6,80 / 0,040 =170 = 1,7 102.
|
La nébuleuse M 57, située à la distance d~2600 a.l de la Terre a un diamètre D =AooBoo =1,3 1013 km.
Sachant que l'oeil voit comme un point tout objet de diamètre apparent inférieur à 3,0 10-4 rad, montrer qu'il peut théoriquement distinguer les points AooBoo.
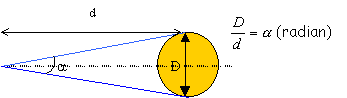
a
: diamètre
apparent
a = 1,3 1013 /(2600 1013) =1,3 / (2*1,3*103) = 0,5 10-3 = 5 10-4 rad, valeur supérieure à 3,0 10-4 rad : l'oeil peut donc distinguer les points extrèmes Aoo et Boo.
En réalit, la nébuleuse M 57 n'est pas observable à l'oeil nu, mais à travers la lunette, elle devient faiblement visible. Proposer une explication.
Il faut prendre en compte le phénomène de diffraction de la lumière.
Quel est, à votre avis, l'intérêt d'utiliser pour les observations, des
lunettes ( et actuellement des télescopes ) qui ont un objectif dont le
diamètre est de plus en plus grand ?
Avec un objectif de grand diamètre, un maximum de lumière entre dans
l'instrument d'optique, ce qui rend les objets observés un peu plus
visibles.
Calculer le diamètre apparent de cette nébuleuse vue à travers la lunette de l'observatoire de Harvard.
a' = G a = 170 * 5 10-4 =0,085 rad.
Lors d'une observation, on place l'oeil derrière l'oculaire dans une zone appelée " cercle oculaire".
Définir le cercle oculaire. Construire le cercle oculaire.
Le cercle oculaire est l'image de la monture de l'objectif donnée par l'oculaire.
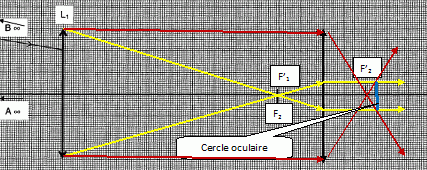
Pourquoi est-il indiqué de placer l'oeil à cet endroit ?
Toute la lumière qui entre dans l'instrument d'optique, pénètre dans l'oeil.
|
|
|
|


