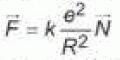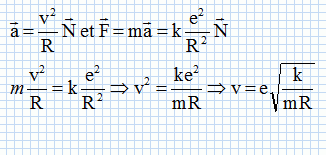|
On se
propose d'étudier
le modèle de l'atome d'hydrogène proposé par Niels Bohr en 1913. Ce
modèle est une continuité du modèle planétaire proposé par Ernest
Rutherford, avec cette différence essentielle que Niels Bohr introduit
un nouveau concept, à savoir la quantification des niveaux d'énergie
dans l'atome.
Mouvement
de l'électron dans l'atome.
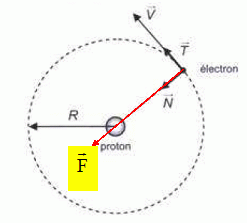
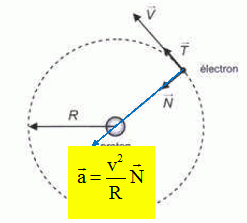
POur commencer cette étude, on suppose que l'électron est animé
d'un mouvement circulaire uniforme de rayon R autour du proton. Les
caractéristiques du mouvement de l'électron sont exprimées dans la base
mobile de vecteurs unitaires N et T comme indiqué sur le schéma :
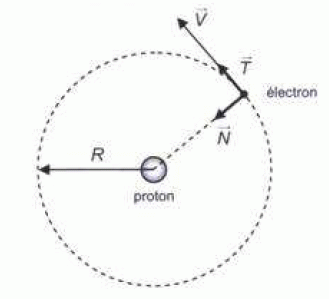
L'électron
est soumis à une force d'interaction électrostatique centripète.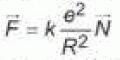
R
: rayon de l'atome ; e valeur de la charge élémentaire et k une
constante.
Représenter sur un
schéma cette force d'interaction.
Déterminer l'unité
de la constante k. ( e s'exprime en coulomb C).
k = F R2 /
e2 ; [k] = N m2 C-2.
Dans le
cas d'un mouvement circulaire uniforme, écrire l'expression du vecteur
accélération.
En appliquant une
loi dont on donnera le nom, montrer que la valeur de la vitesse V est :
V = e [k/(mR)]½.
Ecrire la
seconde loi de Newton suivant l'axe N.
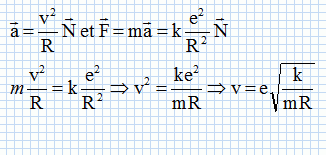
Calculer cette
vitesse.
m = 9,109 10-31 kg ; e = 1,602 10-19 C ; R = 5,3
10-11 m ; k = 9,0 109 SI.
v = 1,602 10-19 [9,0 109 / ( 9,109 10-31*5,3
10-11 )]½ =2,2 106 m/s.
Donner
l'expression de l'énergie cinétique puis la calculer en J et eV.
Ec =½mv2 =½ke2/R =0,5 *9,0 109
*(1,6 10-19)2 / 5,3 10-11
=2,174 10-18 ~2,2
10-18 J.
2,174 10-18 / 1,6 10-19 = 13,6 ~14 eV.
La
quantification de Bohr.
Dans
le modèle de Bohr, l'énergie de l'atome est quantifiée.
Expliquer
ce qu signifie l'adjectif " quantifié".
Seules un petit nombre de valeurs sont possibles pour l'énergie de
l'atome.
Dans la mécanique de Newton, à l'échelle humaine, toutes les valeurs
sont possibles pour l'énergie.
L'énergie de l'atome d'hydrogène se met sous la forme : En =
-13,6 / n2 ( eV).
n est un nombre entier strictement positif appelé nombre quantique
principal.
A chacune de ces énergies est associée une orbite circulaire de
l'électron dont le rayon rn vérifie : rn = a0n2.
a0 est une grandeur appelée " rayon de Bohr", valeur du
rayon de l'atome pour la plus petite valeur de n, à savoir n=1.
Compléter
le tableau suivant :
n
|
1
|
2
|
3
|
4
|
5
|
En
( eV)
|
-13,6
|
-3,40
|
-1,51
|
-13,6
/ 16 = -0,850
|
-13,6
/ 25 = -0,544 |
rn
|
a0
|
4a0 |
9a0 |
16a0 |
25a0 |
Vers
quelle valeur évolue l'énergie En de l'atome lorque
la valeur de n devient très grande ? Même question pour rn.
En tend vers zéro et rn tend vers l'infini.
|
l'image
que l'on peut donner de l'électron en interaction avec le proton de
l'atome d'hydrogène est celle d'un puits dans lequel l'électron serait
"piégé".

Quelle
énergie minimale faut-il fournir à l'atome pour libérer l'électron de
ce puits ?
13,6 eV.
Quelle modification
subit l'atome d'hydrogène si l'électron est libéré de ce puits ?
L'atome perd son unique électron ;
l'atome est ionisé.
On apporte à l'atome, dans son état de plus basse énergie, une énergie DE = 10,2 eV.
Dans
quel état énergétique se retrouve alors l'atome après avoir reçu cette
énergie ?
L'atome gagne de l'énergie et se retrouve dans un état dit "excité".
dans ce nouvel état, l'atome est instable et va chercher à retrouver
son étét de plus basse énergie. Ce phénomène s'accompagne de l'émission
d'un photon.
Déterminer
sa fréquence puis sa longueur d'onde dans le vide.
E =10,2 *1,6 10-19 =
1,632 10-18 J.
E = h n ; fréquence n = E/ h = 1,632 10-18 / 6,62 10-34
=2,47 1015 Hz.
longueur d'onde l = hc /E
= 6,62 10-34 *
3,00 108 / 1,632 10-18
=1,22 10-7 m = 122
nm.
A
quel domaine spectrale appartient la radiation émise ?
122 nm est inférieure à 400 nm, limite entre le visible et le domaine
UV.
122 nm appartient au domaine UV.
|
|