A la découverte d'un minéral radioactif : l'autunite .
Qu'appelle t-on noyau radioactif ?
Un noyau radioactif est un noyau instable dont la
désintégration (destruction) aléatoire
s'accompagne :
L'apparition d'un nouveau noyau
L'émission d'une particule notée
a, b
- ou b +
L'émission d'un rayonnement
électromagnétique noté g.
L'uranium présent dans l'autunite comprend 3 isotopes naturels : 23892U, présent en écrasante majorité, 23592U et 23492U.
Donner la définition de noyaux isotopes.
Des noyaux
isotopes ont le même nombre de charge Z mais des nombres
de nucléons A différents.
Comparer la composition des noyaux d'atomes d'uranium 235 et 238.
23892U : 92 protons et 238-92 =146 neutrons.
23592U : 92 protons et 235-92 =143 neutrons.
|
Voici une petite partie de la chaîne de désintégration de l'uranium 238.
23892U ---> 23490Th --->23491Pa ---> 23492U ---> 23090Th.
Rappeler les lois de conservation dites lois de Soddy, intervenant lors des réactions nucléaires.
Lors d'une désintégration radioactive
a ou b
il y a conservation du nombre de charge Z et du nombre de
nucléons A.
|
Ecrire l'équation de la désintégration du noyau d'uranium 238 en thorium 234.
23892U ---> 23490Th + 42He.
Quel est le type de radioactivité correspondant à cette désintégration ?
Type alpha : émission d'un noyau d'hélium 42He.
Le thorium se désintègre lui même en proactinium 23491Pa.
Ecrire l'équation de cette désintégration.
23490Th ---> 23491Pa + 0-1e.
Quel est le type de radioactivité correspondant à cette désintégration ?
Type ß- : émission d'un électron.
L'uranium 238 présente un temps de demi-vie t½=4,5 109 ans.
Rappeler la définition du temps de demi-vie.
La demi-vie radioactive,(ou période)
notée t½, d'un échantillon de noyaux
radioactifs est égale à la durée au
bout de laquelle la moitié des noyaux radioactifs
initiaux se sont désintègrés.
En utilisant la loi de décroissance radioactive N(t) = N0 exp(-l t), retrouver la relation entre le temps de demi-vie et la consatnte radioactive l : t½= ln2 / l .
N(t½) = N0 exp(-l t½) = ½ N0 ; exp(-l t½) = 0,5 ; -l t½ = ln 0,5 = -ln 2 ; t½= ln2 / l .
En déduire la valeur de la constante radioactive l en an-1 puis en s-1.
l = ln 2 / t½ =ln2 / 4,5 109 =1,54 10-10 ~1,5 10-10 an-1.
4,5 109 ans = 4,5 109*365*24*3600 s = 1,42 1017 s ;
l = ln 2 / t½ =ln2 / 1,42 1017=4,88 10-18 ~4,9 10-18 s-1.
L'activité A0 d'une autunite de masse voisine de 100 g n'est pas négligeable : elle est voisine de 9000 Bq.
Rappeler la définition de l'activité d'une espèce radioactive. Que représente un becquerel ( 1 Bq) ?
L'activité A
d'une source radioactive est égale au nombre moyen de
désintégrations par seconde dans
l'échantillon. Elle s'exprime en becquerels dont le
symbole est Bq (1Bq=1 désintégration par
seconde).
Calculer le nombre de noyaux N0 d'uranium présents dans cette pierre à la date t=0 s et montrer que son ordre de grandeur est de 1021.
A0 = l N0 ; N0 = A0 / l = 9000 / 4,88 10-18 = 1,8 1021.
Quelle est l'activité de la pierre au bout de 100 ans ? au bout de 1000 ans ? Conclure.
A(t) = A0 exp(-l t) ; A(100) = 9000 exp(-1,54 10-10 *100) ~ 9000 Bq.
A(1000) = 9000 exp(-1,54 10-10 *1000) ~ 9000 Bq.
L'activité de cette pierre décroît très lentement , le temps de demi-vie étant de l'ordre du milliard d'années.
Quels effets biologiques peut avoir l'inhalation prolongée de poussières issues de cette pierre ?
L'action sur les tissus vivants
dépend :
du nombre de particules
reçues par seconde. Ce nombre dépend de
l'activité de la source et de son
éloignement.
de l'énergie et de la
nature des particules émises et donc
reçues.
du fractionnement de la dose
reçue.
de la nature des tissus
touchés.
Les particules ionisantes et
le rayonnement g
sont capables de provoquer des réactions chimiques et
des modifications dans la structure des molécules
constituant la matière vivante. En particulier, ils
peuvent induire des mutations génétiques
lorsque l'ADN se trouve modifié.
|
La radioactivité provoquée de l'uranium.
Dans
certaines conditions l'uranium 235 peut se scinder en deux noyaux plus
legers et plus stables comme par exemple le strontium et le xénon selon
l'équation suivante :
23592U +10n ---> 94ZSr + A54Xe + 310n .
CComment appelle t-on ce type de réaction ?
La fission est une
réaction nucléaire provoquée au cours
de laquelle un noyau lourd "fissible" donne naissance
à deux noyaux plus légers. La réaction
se fait avec perte de masse et dégagement
d'énergie.
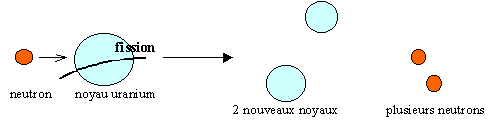
Déterminer la valeur de A et de Z.
Conservation de la charge : 92 = Z+54 d'où Z = 38.
Conservation du nombre de nucléons : 235+1 = 94 +A + 3 d'où A = 139.
Enoncer la relation de l'équivalence masse -énergie.
Un système de masse m
possède lorsqu'il est au repos, une énergie:
E =
m.c2
E: énergie du
système en joules (J) ;
m: masse du système en
kilogrammes (kg) ; c: vitesse
de la lumière dans le vide
(c=3,0.108m.s-1).
Exprimer en fonction des masses des particules et des noyaux intervenant dans l'équation précédente, la variation de masse DE au cours de cette réaction nucléaire. La calculer en J et en MeV.
m(23592U) = 235,120 u ; m(94ZSr)= 93,8946 u ; m(A54Xe) =138,888 u ; m(10n) =1,00866 u.
1 u = 1,660 54 10-27 kg.
DE = (m(94ZSr) +m(A54Xe) + 2m(10n) - m(23592U) ) c2.
DE = (93,8946 + 138,888 + 2 *1,00866 - 235,120 ) * 1,660 54 10-27*(3,00 108)2.
DE = -4,78 10-11 J.
-4,78 10-11 J = -4,78 10-11 / 1,60 10-13 MeV ~ -300 MeV.
Est-ce que de l'énergie est libérée au cours de la réaction ? Justifier.
DE étant négative, de l'énergie est libérée au cours de cette réaction.
|