ondes stationnaires, acoustique musicale. résumé de cours
produire un son, émettre	Instruments de musique : il doit vibrer et émettre. Un excitateur ( corde, anche, membrane frappée...) produit une vibration ; le son est émis grâce à un couplage ( caisse de résonance pour les instruments à cordes, colonne d'air pour les instruments à vent, micro + amplificateur pour les guitatres électroniques) entre l'excitateur et l'air. Modes de vibration d'une corde ou d'une colonne d'air : Une corde tendue entre deux points fixes et soumise à une excitation sinusoïdale entre en résonance lorsque les fréquences excitatrices sont multiples d'une même fréquence f0, appelé mode fondamental. Les fréquences multiples de f0 sont appelées harmoniques. Observée à l'aide d'un stroboscope, la corde prend l'aspect d'un ou plusieurs fuseaux. - les extrémités d'un fuseau sont immobiles : noeuds de vibration. - le milieu d'un fuseau vibre avec une amplitude maximum : ventre de vibration. Lorsque la corde vibre sur le mode n, elle présente n fuseaux. Lorsque qu'une corde pincée ou frappée vibre en oscillationes libres, elle émet une vibration sonore - superposition de vibrations sinusoïdales de fréquences égales à celles du mode fondamental et des modes harmoniques. - la fréquence du son émis est celle du mode fondamental. Une colonne d'air ( instruments à vent ) posséde aussi un mode propre et des modes harmoniques. Les fréquences propres dépendent de la longueur de la colonne d'air : la fréqence du fondamental augmente si la longueur de la colonne d'air diminue ; suivant la nature du tuyau ( ouvert ou fermé) la colonne d'air assure un couplage sélectif ( elle n'émet que les vibrations dont les fréquences sont celles de ces modes propres, contrairement à la caisse de résonance d'un instrument à corde).
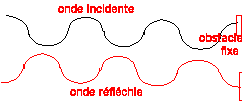
ondes stationnaires	réflexion d'une onde sur un obstacle unique : Lorsqu'une onde rencontre un obstacle rigide, elle produit une onde réfléchie : La superposition d'une onde progressive sinusoïdale de fréquence f et de l'onde réfléchie sur un obstacle fixe produit une onde stationnaire : une vibration sans propagation, de fréquence f. - une seule réflexion ne fait pas apparaître de condition sur la fréquence ( pas de quantification sur la fréquence). - la distance entre deux points immobiles (noeuds de vibration ) est égale à une demi-longueur d'onde de l'onde incidente : d = ½l. propagation d'une onde entre deux points fixes : Soit une onde sinusoïdale se propageant, sans atténuation, sur une corde tendue entre deux points fixes distants de L. L'onde subit une réflexion sur chaque extrémité. Le phénomène est périodique de période ( durée d'un aller et retour - menu) T0 = 2 L/v ( célérité de l'onde). Pendant cette durée l'onde s'est propagée d'une longueur 2L à la célérité v. Les deux extrémités fixes sont des noeuds de vibrations : les ondes stationnaires s'établissent si la longueur L de la corde est un multiple de la demi-longueur d'onde l. On observe au milieu de chaque fuseau un ventre de vibration d'amplitude supérieure à 2 a ( a :amplitude de la source) L= n ½ l ou 2L = nl avec n : nombre de fuseaux stables sur la corde de plus l = v /f soit f = n v /(2L) Les fréquences des ondes stationaires qui peuvent se propager sur une corde tendue entre deux points fixes sont les fréquences propres de vibration de la corde. Comme sur une corde tendue, il peut s'établir, dans une colonne d'air excitée par une vibration sinusoïdale, un système d'ondes stationaires résultant de la superposition des ondes réfléchies aux extrémités de la colonne.
acoustique musicale	L'oreille humaine perçoit les sons dont les fréquences sont comprises entre 20 Hz et 20 000 Hz. Un son est d'autant plus aigu que sa fréquence est plus grande ; d'autant plus grave que sa fréquence est plus petite. L'intensité sonore, exprimée en W m-2, correspond à l'énergie sonore reçue par l'oreille. I0 =10-12 W m-2 constitue le seuil d'audibilité. Pour une intensité I, la sensation physiologique du son est traduite par le niveau sonore, noté L, exprimé en décibel (dB) : L= 10 log(I/I0). Si l'intensité sonore double, le niveau sonore augmente de 3 dB. Le seuil de la douleur correspond à 100 dB. Le sonomètre mesure le niveau sonore. Un son musical est défini par : Sa hauteur, caractérisée par sa fréquence du fondamental. Son intensité, liée à l'amplitude de l'onde mécanique responsable de l'onde. Son timbre ( il dépend de la composition des harmoniques) permet de distinguer deux notes de même hauteur jouée par deux instruments différents. Les gammes : Si une note a une fréquence double d'une autre, ces deux notes sont séparées d' une octave. La gamme tempérée est divisée en douze intervalles égaux appelés demi-tons. Le rapport des fréquences est le même entre deux notes successives 2 1 /12.
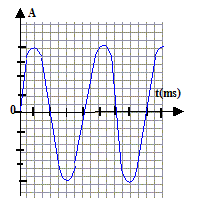
Un orchestre	Le timbre ( il dépend de la composition des harmoniques) permet de distinguer deux notes de même hauteur jouée par deux instruments différents. ce son ( flûte) est complexe, somme de sinusoïdes. période T = 2,3 10-3 s ; fréquence f= 1/T = 435 Hz. ce son est pur : une seule sinusoïde La hauteur , caractérisée par sa fréquence du fondamental. 1 2 Les sons ci-dessus, joués par deux instruments différents ont la même période, la même fréquence du fondamental, donc la même hauteur. 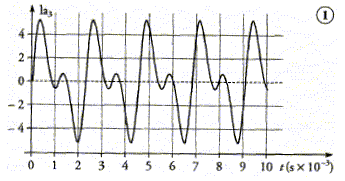L'amplitude du son 1 est supérieure à l'amplitude du son 2 : le son 1 est plus intense. Les deux instruments n’ont pas le même timbre : l'allure des deux courbes conduit à des harmoniques différentes. L'intensité sonore, exprimée en W m-2, correspond à l'énergie sonore reçue par l'oreille. I0 =10-12 W m-2 constitue le seuil d'audibilité. La sensation physiologique du son est traduite par le niveau sonore, noté L, exprimé en décibel (dB) : L= 10 log(I/I0). soit I= I0 10-L/10. Lorsqu' un instrument A émet un son, le niveau sonore vaut LA = 70 dB. L'intensité acoustique vaut : IA= I0 10-7 Wm-2. Si deux instruments identiques à A émettent simultanément le même son, les intensités acoustiques s'ajoutent : I1 = 2 IA et le niveau sonore devient : L1= 10 log (2IA/I0) = 10 log (IA/I0) + 10 log 2 = 70 +3 = 73 dB. Lorsqu' un instrument B émet un son, le niveau sonore vaut LB = 60 dB. L'intensité acoustique vaut : IB= I0 10-6 Wm-2. Les intensités acoustiques s'ajoutent I2 = IA+IB=I0 10-7+I0 10-6 =1,1 I0 10-6 =1,1 IB Wm-2. Le niveau sonore devient : L2= 10 log (1,1 IB/I0) = 10 log (IB/I0) + 10 log 1,1 = 60 +0,4 = 60,4 dB. Le seuil de la douleur est fixé à 100 dB. Le niveau sonore du son émit par l'orchestre ne dépasse pas cette valeur. Tension délivrée par un microphone correspondant au son émis par la corde n°5 d’une guitare accordée sur le " la1 ". 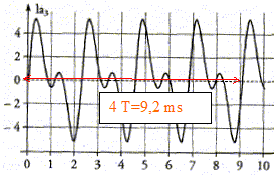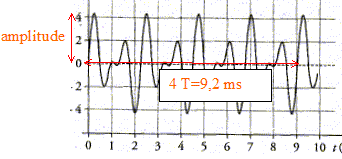5 T = 4,5 10-2 s soit T= 9 ms = 9 10-3 s ; fréquence du fondamental : f0= 1/T = 111 Hz. Hauteur du son : 111 Hz. Les fréquences multiples de f0 sont appelées harmoniques : f1 = 222 Hz ; f2 = 333 Hz ; f3 = 444 Hz. La longueur de la corde de guitare émettant cette note est L= 65,2 cm ; cette corde présente un seul fuseau. la longueur d'onde l de la vibration vaut 2L= 1,30 m ; la célérité de l'onde est : v = l f = 1,3 * 111 = 144 m/s. Une longueur différente de cette même corde émet un son de fréquence f= 150 Hz. La tension de la corde ainsi que sa masse linéique n'ont pas changé : en conséquence la célérité du son est conservée. Or v = l f : si f augmente ( à v = constante) alors l =2L diminue ; la corde est plus courte.
	retour - menu