oscillateur mécanique cours exercices
le mouvement de l'oscillateur peu amorti est périodique
la période
équation différencielle
exercice 1 bande passante d'un oscillateur mécanique Pour étudier un oscillateur mécanique, on mesure l'amplitude x de ses oscillations en fonction de la fréquence f de son excitateur. On obtient le tableau suivant: f(Hz) 0,4 0,6 0,8 1 1,1 1,22 1,24 1,28 1,32 1,34 1,4 x(cm) 1 1,3 1,6 2,3 3,5 9,5 12,1 13,4 11,9 9,5 5 la largeur de la bande passande de cet oscillateur est : 1,28Hz ; 3,9 cm ; 0,12 Hz ; 2hz ; 9,5 hz corrigé amplitude maximale : 13,4 cm( phénomène de résonance) bande passante : ensemble des fréquences telles que l'amplitude soit supérieure à 9,5 cm soit (13,4 / 1,414) 1,34-1,22 = 0,18 Hz exercice 2 fronde assimilé à un pendule simple Une fronde est constituée d'un fil inextensible , de masse négligeable, de longueur l=50 cm, et d'un petit solide de masse m=20g, fixé à l'une de ses extrémité. L'amplitude angulaire est 10° La période des oscillations est voisine de 1,4 s(répondre vrai ou faux) La période de ce pendule simple est indépendante de l'amplitude , car celle ci est petite. La masse ayant un mouvement circulaire , le produit vecteur vitesse scalaire vecteur accélération est nul. On fait tourner le dispositif dans un plan verticale à la façon d'une fronde. Au point le plus bas la vitesse est notée v0. Pour que la rotation ait entierement lieu, il faut que v0 soit au moins égale à 3,2 ms-1. 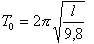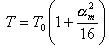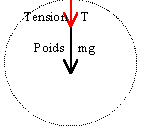corrigé la période est 6,28*0,2258=1,42 s vrai si l'amplitude angulaire est inférieure à 20° ou 0,35 rad vecteur vitesse et vecteur accélération sont perpendiculaires si le mouvement est circulaire et uniforme Soit v la vitesse minimale au point le plus hau t. La seconde loi de Newton s'écrit , suivant l'axe n de la base de Frenet . T + mg=m v2/ longueur Pour atteindre le point le plus haut, le fil restant tendu , la tension est positive ou nulle . La vitesse minimale au point le plus haut est donc gl=v2 conservation de l'énergie mécanique : 0,5m v20=0,5mv2+g*2l donc v20=v2+4gl=5gl soit une vitesse v0 minimale de 4,94 ms-1 exercice 3 oscillateur mécanique horizontal On néglige tout frottements. La constante de raideur du ressort est égale à 10N /m. La masse du solide fixée à une extrémité du ressort est 100g. A partir de l'équilibre on exerce une force horizontale de valeur 1 N à l'extrémité du ressort, la longueur de celui ci devient alors égale à 10 cm vrai ou faux On considère l'oscillateur en mouvement. A l'instant t, le solide possède la vitesse v , l'énergie potentielle de l'oscillateur est donc égale à E=Ep=K-0,5mv2 où K est une constante La période des oscillations est voisine de 0,63 s. Comme il n'y a aucun frottements, on peut dire que les oscillations sont entretenues. corrigé faux la déformation du ressort ou allongement est de 10 cm (la déformation et la force sont proportionnelles vrai énergie mécanique initiale 0,5 * k *amplitude2 énergie mécanique à la date t : E=0,5mv2+ 0,5k x2 conservation de l'énergie mécanique 6,28*0,1=0,628 s faux aucun dispositif d'entretien oscillations libres sinusoidales exercice 4 l'horloge entretenue. Une horloge est constituée d'un pendule simple entretenu de période propre 2 s. Pour maintenir l'amplitude des oscillations constante, l'horloge puise son énergie dans l'énergie potentielle d'une masse de 1 kg descendant d'une hauteur de 1 m par semaine. g=9,8 m s-2. longueur du pendule l= 1 m. Evaluer le travail des frottements au cours d'une oscillation. La longueur d'un pendule simple peut varier avec la température. Quel est l'allongement Dl acceptable pour que l'horloge indique encore l'heure exacte à 10 secondes près au bout d'un jour de fonctionnement. 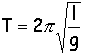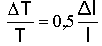corrigé Energie potentielle stockée par cette masse : m g h =1* 9,8 *1 = 9,8 J une semaine =7*24*3600=604 800 s ou 302 400 oscillations travail des frottements = opposé de l'énergie utilisée à chaque période pour entretenir le pendule - 9,8/ 302 400= 3,24 10-5 J période du pendule simple dérivée logarithmique de la période DT/T=10/(24*3600)=1,157 10-4 ; Dl =2*1,157 10-4 = 2,3 10-4 m exercice 5 pendule conique 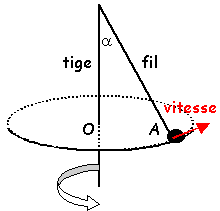Une masse m=0,1 kg ponctuelle est attachée à un fil inextensible de longueur l=1 m. La masse tourne autour de la tige et l'angle a est constant a=22,5° ; g=9,8 ms-2 . Quelle est la vitesse angulaire w en rad s-1 ? Quelle est la tension du fil ? Quelle est la valeur de la vitesse v ? Pour quelle valeur minimale de w le fil commence t-il à se détacher de la tige verticale ? 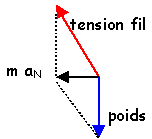corrigé L'accélération est centripète dirigée vers O de valeur aN =v²/OA = w²*OA avec OA=l sin(a) tan(a)= m aN / mg voir schéma ci contre tan(22,5)= w² sin(22,5)/9,8 ou bien 1/cos(a)= w²/9,8 ou bien w²=9,8 / cos(22,5)=10,6 ; w=3,26 rad s-1.     tension du fil T= mg/cos(a) = 0,1*9,8/cos(22,5)= 1,06 N vitesse de A v=w*OA=w*l sin(a)= 3,26*sin(22,5)= 1,25 ms-1. valeur minimale de la vitesse angulaire cos(a)=9,8/ w² voir ci dessus Lorsque le fil commence à se détacher de la tige verticale , l'angle vaut encore 0 et cos(0)=1 d'où la valeur minimale de la vitesse angulaire : w²=1/9,8 ; wminimale=3,13 rad s-1. exercice 6 dilatation et période d'un pendule Un balancier d'horloge est constitué d'une tige d'un alliage de cuivre qui oscille autour d'un axe horizontal passant par l'extrémité supérieure de la tige. A l'extrèmité inférieure est fixée une lourde masse de bronze. La température augmente de 20°C. (vrai ou faux) loi de la dilatation L=L0(1+aT) ; a positif; L et L0 longueur à t°C et 0°C ; T température en Kelvin ;T(K)=273+ température en °Celcius. L'horloge retarde. La masse du pendule change. Le poids du pendule change. L'horloge avance. corrigé vrai Le balancier est assimilé à un pendule simple. Sa période est proportionnelle à la racine carrée de la longueur. Celle ci augmente avec la température. L'horloge retarde. faux La masse est invariable. faux le poids varie avec l'altitude et dépend de la position où l'on se trouve par rapport à une planète. 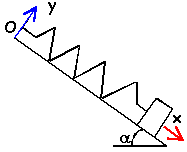exercice 7 ressort sur plan incliné -abscisse et vitesse raideur k=10Nm-1 ; longueur ressort à vide 20 cm ; masse fixée au ressort m=100 g ; angle a=45° ; g=10 ms-2. On écarte le ressort de 2 cm de sa position d'équilibre vers le bas et on le lache sans vitesse à l'instant t=0. Quelle est la pulsation de cet oscillateur ? Exprimer en fonction du temps l'abscisse du centre d'inertie G de la masse fixée au ressort. Exprimer en fonction du temps la vitesse de G . Exprimer en fonction du temps l'énergie mécanique du système masse ressort. 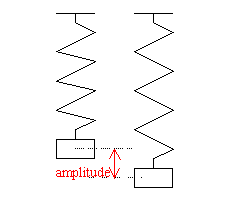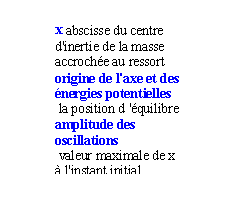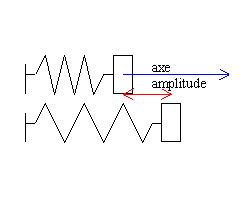corrigé L'origine des énergies potentielles est la position d'équilibre du ressort. w²=k/m=10/0,1 =100 w=10 rad s-1 abscisse =amplitude fois cos(wt+j) x= 0,02 cos(10t+j) à la date t=0 x=0,02 mètre 0,02=0,02 cos(j) alors j=0....x= 0,02 cos(10t) vitesse =dérivée de l'abscisse par rapport au temps x'=v= 0,02 *10*(-sin(10t)) v= -0,2 sin(10t) E méca =E potentielle +E cinétique 0,5 kx²+ 0,5 mv²= 0,5 k amplitude²=constante (absence de frottements) E=0,5[ 4 10-3cos²(10t) + 0,1*4 10-2 sin²(10t)]= 2 10-3 J exercice 8 ressort :équation horaire - travail à fournir Un ressort de raideur k=10 Nm-1 peut se déplacer le long d'un axe horizontal. L'une de ses extémité est fixe . A l'autre on accroche un solide S de mase m=0,1 kg. L'origine des énergies potentielle est la position d'équilibre du ressort.Il oscille avec une amplitude de 4 cm, sans vitesse initiale. (répondre vrai ou faux) L'équation horaire du centre d'inertie G de S est : x=0,04sin(10t) La vitesse maxi est 0,4 m s-1. Le travail fourni pour allonger le ressort de 2 cm est 2 mJ. On allonge le ressort de 2 cm de plus; le travail supplémentaire à fournir est 4 mJ. corrigé faux la vitesse est la dérivée de l'abscisse x par rapport au temps soit 0,04*10*(cos(10t)). Donc à t=0 la vitesse vaut 0,4 m s-1 en contradiction avec le texte. x=0,04cos(10t) est correct vrai expression de la vitesse v=x'=0,04*10*(-sin(10t)). la valeur maxi est bien 0,4 m s-1 à t=0,25 période par exemple vrai Le travail fourni se retrouve sous forme d'énergie potentielle élastique stockée par le ressort. 0,5*10*0,02²=2 mJ faux la déformation totale du ressort est 0,04 m 0,5*10*0,04²=8 mJ donc 6 mJ de plus pulsation w²=k/m w=rac carrée (10/0,1) =10 rad s-1. énergie potentielle élastique 0,5 k x² exercice 9 : Un mobile auto porteur de masse m=350g est accroche en A un ressort horizontal dont l'autre extremite B est fixe. Le mobile se deplace sans frottement, un dispositif de guidage contraint son cenre d'inertie G a ne se deplacer que selon un axe x'x passant par A et B. On utilise un ressort R1 et on mesure une periode T1=0,5s. En deduire la raideur K1 du ressort. Calculer l'énergie mécanique totale E1 du système lorsque le mobile effectue des oscillations d'amplitude Xm=3cm, en considérant comme nulle l'energie mécanique du système immobile dans sa position d'equilibre. - en déduire, pour des oscillations de cette amplitude, la vitesse du mobile lorsqu'il repasse par la position d'équilibre. On souhaite obtenir des oscillations de période T2=2T1 en remplacant le ressort R1 de raideur k1 par un ressort R2 de raideur K2. - calculer k1/K2 . - calculer l'amplitude des oscillations du système fonctionnant avec le ressort R2 pour que son énergie mécanique conserve la valeur E1 calculée ci-dessus . - Quelle sera alors la vitesse du mobile au passage par la position d'équilibre ? 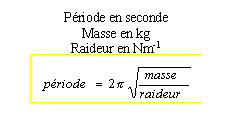corrigé : T = 6,28 racine carrée ( masse / raideur ressort) 0,5 ² = 6,28 ² * 0,35 / K1 K1 = 55,2 N/m. énergie mécanique : 0,5 fois raideur fois amplitude au carré= ½K1a² 0,5 *55,2 * 0,03 ² = 0,025 J. au passage à la position d'équilibre l'énergie est sous forme cinétique 0,5 m v² v = rac carrée(0,025 *2 / 0,35 )= 0,376 m/s. si la période double : la raideur doit diminuer car elle intervient au dénominateur en tenant compte de la racine carrée la nouvelle raideur doit être égale à K2 = K1 / 4 K1 / K2 = 4 ou K2 = 55,2 / 4= 13,8 N/m. nouvelle amplitude : 0,025 = 0,5*13,8 X² X = 0,06 m. vitesse de passage à la position d'équilibre inchangée car énergie mécanique inchangée.
retour - menu