Ondes:

1. On étudie la propagation d'une perturbation le long d'une corde élastique. La figure 1 ci-dessous indique la forme de la perturbation qui se propage et les vecteurs vitesse V_A et V_B de deux points A et B de la corde à une date déterminée.
   - Quel est le sens de propagation de la perturbation ? justifier la réponse.
2. Ondes sonores et ondes radio :
   On étudie la mise à feu de deux charges explosives situées en deux points A et B par un signal radio émis par un émetteur E ; L'observateur est situé au point O (la figure 2 ci-dessous donne les positions des différents points).L'observateur en O perçoit deux explosions. Quelle est la durée qui les sépare si :
   - On suppose la propagation du signal radio quasi instantanée ?
   - On tient compte de la célérité du signal radio ?
   Données: Célérité du signal radio dans l'air : c=300 000km/s et celle du son dans l'air : v=330 m/s. AB=BE= 5km
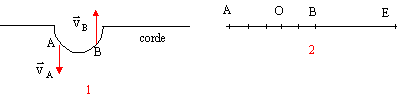
3. La fondre est une décharge électrique frappant la Terre qui s'accompagne d'une émission lumineuse (l'éclair) et d'une émission sonore (le tonnerre). Soit d la distance séparant le lieu de l'orage de l'observateur ; on note Dt la durée séparant la perception du tonnerre de celle de l'éclair.
   - Exprimer la distance d en fonction de v et de D t si on considère la propagation de la lumière comme pratiquement instantanée.
   - Sans faire aucune simplification, exprimer la distance d en fonction de c, v et D t.
   - Mettre l'expression de d sous la forme :D= (vDt)/(1 - v/c )
   - Montrer que le rapport v/c est nettement plus petit que 1 ; simplifier l'expression obtenu à la question c pour retrouver le résultat de la question a.
   - Calculer la valeur de d pour D t=5,2 s.

   Données : Célérité du signal radio dans l'air : c=300 000km/s et celle du son dans l'air : v=340 m/s.

simulation d'une hola :

La hola dans un stade peut être assimilée à une corde. Dans une classe, on effectue une simulation de hola.
- Un chemin a été défini pour la propagation de la hola.
- Chaque élève atteint par la hola effectue les opérations suivantes (soit d la distance entre deux élèves consécutifs) : a : il se lève ; b : il reste debout quelques instants ; c : il s'assoit.
- Un élève marque le rythme en prononçant fortement et régulièrement les lettres a, b, c.
- Quelques élèves observent et notent leurs commentaires.

1. Propagation d'un hola unique.
   A l'énoncé des lettres a, b, c, le premier élève effectue la suite des opérations, puis le deuxième ……
   - Chaque élève a-t-il un mouvement périodique ?
   - Que peut-on dire du mouvement d'un élève déterminé par rapport au mouvement du premier élève ?
2. Propagation d'un hola périodique
   L'élève continue à énoncer les lettres a, b, c mais à intervalles réguliers (abc, abc, abc,….), un signal est donné (par exemple par un coup de règle sur un table) et la hola repart du premier élève. Attention, chaque participant doit faire preuve de concentration et éviter de se tremper. On laisse progresser cette " hola périodique " et on l'arrête sur un b (marqué par un autre coup de règle), date où certains élèves sont debout (et restent debout).
   - Chaque élève a-t-il un mouvement périodique ? Si oui, évaluer cette période T en fonction de la durée t_a séparant deux a consécutifs.
   - Lors de l'arrêt, observe-t-on une période spatiale ? Justifier la réponse.
   - Lors de l'arrêt, quelle est la distance séparant deux élèves consécutifs qui sont debout ? Evaluer cette distance en fonction de l'intervalle entre deux élèves. Quelle grandeur mesure-t-on ainsi ?
   - Quel temps met la hola pour parcourir la distance séparant deux élèves consécutifs qui sont debout ? Conclure. 

mesure de la célérité du son :

Le son émis par le haut parleur est capté par deux microphones M₁ et M₂ branchés sur les voies Y_A et Y_B de l'oscilloscope. On voit deux courbes en phase ; chaque courbe représente deux périodes ; l'écran mesure 10 cm de large ; sensibilité 0,1 ms/cm.

1. Calculer la fréquence du son capté par les microphones.
2. Les abscisses x₁ et x₂ des deux microphones sont repérées sur la règle. Lorsque x₁=x₂=0 les courbes observées sur l'oscilloscope sont en phase. On laisse le microphone M₁ en place et on déplace lentement le microphone M₂. On relève l'abscisse x₂ de ce microphone à chaque fois que les courbes sur l'oscilloscope sont de nouveau en phase. Les positions correspondantes sont données dans le tableau ci-dessous

   position n°	1	2	3	4	5
   abscisse x2 (cm)	17	34	51	68	85

   -Quelle valeur de la longueur d'onde de l'onde sonore peut-on déduire de ces mesures ?
   -Quelle est la célérité du son dans l'air à la température où sont effectuées les mesures ?
3. Le son émis par le haut parleur est capté par le microphone M. On réalise les deux branchements sur l'oscilloscope ( haut parleur sur la voie 1 et microphone sur la voie 2)
   - Quelles sont les deux tensions visualisées sur l'oscilloscope ?
   - Quelle est la fréquence du son sachant que la rapidité de balayage est de 0,2 ms/cm ? (on observe deux périodes sur l'écran)
   - On déplace le microphone M jusqu'à obtenir, sur l'écran de l'oscilloscope, deux sinusoïdes en phase. L'abscisse sur la règle est alors x₁=4,5 cm. Puis on déplace le microphone le long de la règle ; la sinusoïde de la voie Y_B se décale alors progressivement par rapport à celle de la voie Y_A. Lorsque le microphone se trouve à l'abscisse x₂=38,5 cm, les deux sinusoïdes se trouvent de nouveau en phase. Quelle est la valeur de la longueur d'onde de l'onde sonore dans l'air dans ces conditions ? Justifier la méthode. En déduire la célérité des ondes sonores dans l'air. 

diffraction par une fente

1. Le laser hélum-néon émet une lumière rouge pratiquement monochromatique de longueur d'onde l=633nm. Une fente de largeur a est placée sur le trajet du faisceau lumineux produit par le laser. Un écran est placé à la distance D=2,50 m de la fente. On déplace une cellule photoélectrique le long de l'axe x'x (O est le point d'incidence du faisceau en l'absence de fente). Cette cellule est alors une source de tension u proportionnelle à l'intensité lumineuse en chaque point M de l'axe x'x, d'abscisse OM=x.

   x mm	+/-26	+/-24	+/-22	+/-20	+/-18	+/-16	+/-15	+/-14	+/-13	+/-12	+/-11	+/-10	+/-9	+/-8	+/-7	+/-6	+/-5	+/-4	+/-2	+/-0
   u(V)	0,2	0,1	0	0,2	0,6	0,7	0,6	0,5	0,2	0	0,2	0,7	1,3	2	2,4	3,3	3,8	4,3	4,7	4,8

2. Tracer la courbe représentant les variations de la fonction u=f(x), pour les valeurs de x comprises entre -26 mm et + 26 mm. Interpréter l'allure de la courbe précédente.
3. La largeur l de la tache centrale de la figure de diffraction observée sur l'écran est : l=2lD/a .Evaluer alors la largeur a de la fente. 

---

corrigé

---

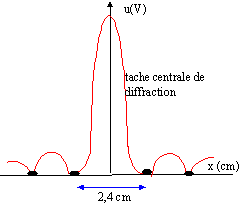
l = 2,4 10^-2 m

diffraction : on observe une tache centrale brillante et de part et d'autre une alternance de taches sombres et de taches de moins en moins brillantes.

a = 2lD / l =2*6,33 10^-7 * 2,5 / 2,4 10^-2 = 1,32 10^-4 m.

---

diffraction d'ondes :

1. Une source lumineuse monochromatique, de longueur d'onde l, et ponctuelle est placée devant une fente de largeur a, sur l'axe de cette fente, à la distance d=20cm de la fente. Un écran se trouve à la distance D=50cm derrière la fente.
   - Déterminer la largeur de la zone éclairée de l'écran (dans la direction perpendiculaire à SA) dans les deux cas suivants : l =600 nm et a=4,0 cm ; l =600 nm et a=0,10 mm.
2. Un haut parleur est placé devant une large planche percée d'une fente de largeur a=3,0 cm, dans l'axe de la fente. Le haut parleur est branché sur un générateur basse fréquence réglé sur la fréquence f=500 Hz.
   -Y a-t-il diffraction des ondes sonores à la traversée de la fente ? Justifier la réponse.
   - Si oui, comment le phénomène se manifeste-t-il ?
   - Derrière la fente, on place un microphone dont on relie les bornes à l'entrée Y_A d'un oscilloscope réglé sur la rapidité de balayage 1 ms/div. Faire le schéma de l'écran de l'oscilloscope sachant que, horizontalement, il comporte 10 divisions. On justifiera tous les points du raisonnement.
   - Qu'observe-t-on en déplaçant le microphone :+
   * En restant à la même distance de la fente ?
   * En s'éloignant de la fente ?
   Données :Célérité des ondes sonores dans l'air : v=340m/s.

Un pointeur optique à laser a la forme et la taille d'un gros stylo. Le faisceau lumineux qui en sert, lorsqu'il est dirigé en direction d'un tableau, donne un point d'impact rouge très lumineux et de petites dimensions. Il permet à un conférencier, même lorsqu'il se trouve très loin du tableau, de pointeur un endroit précis d'un document projeté. On veut retrouver expérimentalement l'ordre de grandeur de la longueur d'onde l₀ de la lumière émise par le pointeur optique à laser (longueur d'onde indiquée dans la fiche technique : l₀ comprise entre 660 et 680nm ).

On utilise le montage suivant : une fente verticale, de largeur a très petite, est placée sur le trajet du faisceau lumineux produit par le laser et un écran est placé à la distance D de la fente.

1. Recopier la phrase suivante en la complétant : " Le phénomène qui se manifeste s'appelle ……. ; son importance est liée au rapport de la largeur a de la fente à ……… ".
2. On propose quatre expressions pour la largeur l de la tache centrale :
   (a) : l= (2lD)/a (b) : l= 2aD/l (c) : l= 2D²/la (d) : l= (2la)/D
   et on réalise trios expériences :
   

   expérience	source	distance D	largeur a	largeur tache centrale l
   n°1	source l1= 543 nm	D	a	l1=3,2 cm
   n°2	source l0	D	a	l2=4 cm
   n°3	source l1= 543 nm	D	a3 < a	l3>l1.

   
   - Par une analyse dimensionnelle, montrer qu'une des expressions est manifestant fausse.
   -A partir des expériences, déterminer les autres expressions que l'on doit éliminer (on précisera à chaque fois les expériences prises en compte). En déduire l'expression de la largeur l de la tache centrale.
   - Etablir la relation entre l₁, l₂, l₁ et l₀. Calculer avec le bon nombre de chiffres significatifs, la valeur numérique de l₀. Ce résultat est-il en accord avec la notice technique du pointeur optique à laser ?