|
diffraction
des ondes
fiche
bac
|
|
pointeur
laser :
Le faisceau lumineux d'un pointeur laser sort par un
diaphragme circulaire de diamètre d1=2mm.
Le fréquence de la lumière émise, quasi
monochromatique est f=4,48 1014 Hz. Il produit,
sur un écran blanc situé à la distance
L = 6m de l'ouverture. Une tache lumineuse de
diamètre d2=12 mm. La puissance lumineuse
émise est P = 3 mW.
- Quelle est la longueur d'onde de la radiation
émise ? Quelle est la couleur de la tache
observée sur l'écran ?
- Quel est l'angle total a
de la divergence de ce faisceau ? Faire un
schéma.
- On considère une onde plane, monochromatique,
de fréquence f qui traverse une ouverture
circulaire de diamètre a. La direction de
propagation est normale au plan de l'ouverture. Au
delà du trou, les surfaces d'onde sont quasiment
sphériques et contenues dans un cône d'angle
au sommet a.
- Quel est le phénomène qui affecte l'onde
lumineuse lorsqu'elle traverse le trou ?
- Quel est la valeur de a ? Comparer a à
d1.
- Peut-on interpréter la divergence du faisceau
lumineux émis par le pointeur ?
- On admet que l'onde qui arrive sur l'écran
situé à la distance L de la sortie du
pointeur est quasiment plane et l'énergie est
conservée pendant la propagation.
- Quel est l'expression de l'aire S de la surface d'onde
en fonction de a, L et d1 ?
- Exprimer la puissance E présenté par
unité de surface d'onde en fonction de P, a, L et
d1.
- Pour cette valeur de la fréquence, le maximum
d'exposition permis par la cornée de l'œil
humain, est égal à 2,5 W.m-2. A
quelle distance de pointeur l'observation directe du
faisceau lumineux, émis par le pointeur,
n'est-elle plus dangereuse
?
corrigé
longueur d'onde (m) = célérité
(m/s) / fréquence (Hz) = 3 108 * 4,48 1014=
0,67 10-6 m (rouge)
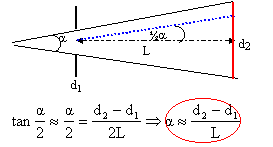
a voisin de : (12-10)10-3/6
=1,67 10-3 rad.
diffraction de l'onde lumineuse à la
traversée d'un trou dont les dimensions sont de
l'ordre de grandeur de la longueur d'onde.
a voisin de d1.
la divergence du faisceau laser peut être due
à la diffraction
aire de la surface : S = pd2²/4
avec d2=d1 +aL
S = p/4 (d1
+aL )²
puissance par unité d'aire : P/S = 4P / (
p (d1 +aL
)² )
2,5 p (d1
+aL )² =4P=
4*310-3.
(d1 +aL )² =
4*310-3/( 2,5 p ) =
1,53 10-3.
d1 +aL = 3,91
10-2.
L= (3,91 10-2- 2 10-3 ) /
1,67 10-3
=22,2
m.
|
|
mesure de l'épaisseur
d'un cheveu :
On dispose d'un laser hélium-néon de
longueur d'onde l =632,8 nm et de
puissance P = 2,0 mW.
On interpose une fente fine verticale entre le laser et
un écran E. Sur l'écran, on observe, dans la
direction perpendiculaire à la fente, une tache
lumineuse centrale de largeur d nettement supérieure
à la largeur a de la fente, ainsi qu'une série
de taches lumineuses plus petites de part et d'autre de la
tache centrale. La distance entre la fente et l'écran
est D=1,60 cm.
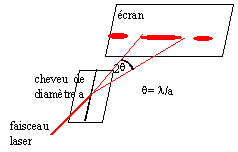
- Faire un schéma de l'expérience et
nommer le phénomène observé.
- Quelle précaution doit on prendre pour
travailler en toute sécurité pendant cette
expérience ?
- Lors de deux expériences, on mesure pour la
tache centrale : une longueur d1=5,0 cm avec
une fente de largeur a1=0,04 mm. et une
longueur d2=2,0 cm avec une fonte de largeur
a2=0,10 mm. Montrer que ces résultats
sont en accord avec la relation : d=2lD/a
- On remplace la fente fine par un cheveu tendu
verticalement sur un support. Pour la même distance
D du fil à l'écran, on observe une figure
analogue à celle obtenue avec la fente et on
mesure d=2,6 cm pour la largeur de la tache centrale. En
admettant que la relation donnée à la
question précédente reste valable pour le
cheveu, calculer son diamètre a.
- On utilise maintenant un laser de même longueur
d'onde l = 632,8 nm mais de
puissance P = 1,0mW. Quelle est, pour le cheveu, la
largeur de la tache lumineuse centrale ? Choisir en
justifiant, la bonne réponse parmi les
propositions suivantes :
a) 1,3 cm b) 2,6 cm c) 5,2 cm.
corrigé
diffraction par le cheveu
il ne faut pas diriger le laser vers les yeux.
ad = 2l D = constante pour
l et D fixés.
a et d sont inversement proportionnelles.
a1 d1 = 0,04*50 = 2 mm²
a2d2 = 0,1*20 = 2 mm²
a*26 = 2 d'où le diamètre du cheveu : a =
2/26 = 0,077 mm = 77
mm.
si la puissance du laser diminue,( les autres
paramètres étant inchangés) la tache de
diffraction sera moins lumineuse mais gardera la même
largeur 2,6 cm.
|
|
pouvoir de résolution
d'une lunette astronomique :
L'onde lumineuse (de longueur d'onde dans le vide
l0 ) émise par
un laser arrive perpendiculairement sur un écran E',
percé d'un trou de rayon r. Elle subit alors une
diffraction. Un écran E est placé à une
distance D derrière E', parallèlement à
ce dernier. Sur l'écran E, on observe non pas une
tache de rayon r, mais une tache circulaire de rayon
R=1,22Dl0/r
entourée d'anneaux concentriques de plus faible
intensité.
- Calculer R si l = 520 nm
et r=4,00 cm. Commenter la valeur obtenue.
- On considère que la lumière
émise par une étoile est monochromatique,
de longueur d'onde dans le vide l0=520nm.
Quand on observe l'étoile avec une lunette
astronomique, la lumière entrant dans la lunette
est diffractée par l'objectif, qui forme une
ouverture circulaire de rayon r. L'objectif est une
lentille mince convergente de distance focale f=0,80m.
Dans le plan focale image de l'objectif, au lieu
d'observer un point, image de l'objet " étoile ",
on observe une tache de diffraction de rayon
R'=1,22fl0/r .
Calculer R' pour r=4,00cm puis pour r=0,5 cm.
- La lunette est maintenant utilisée pour
observer deux étoiles voisines, émettant
des radiations lumineuses de même longueur d'onde.
Elle sont vues depuis l'objectif sous un diamètre
apparent a. En l'absence de
diffraction, on observait dans le plan focal image de
l'objectif 2 points A et B, distants de fa.
En réalité, on obtient une tache de
diffraction pour chaque étoile, l'une de centre A,
l'autre de centre B. On admet que ces taches (et donc les
étoiles) peuvent être distinguées si
la distance entre leurs centres est supérieure
à leur rayon.
-Calculer pour r=4,00cm et pour r=0,5cm, la plus petite
valeur du diamètre apparent a
entre deux étoiles que l'on peut distinguer avec
cette lunette. Cette valeur minimale de a
permet de définir le pouvoir de résolution
de la lunette astronomique. A-t-on intérêt
à utiliser un objectif de grande ou de petite
taille ?
corrigé
R=1,22Dl0/r =
1,22*5,2 10-7 D/0,04 = 1,59 10-5 D
si D= 10 m alors R voisin de 0,16 mm : la diffraction
n'existe quasiment pas, le rayon du trou étant bien
trop grand par rapport à la longueur d'onde.
R=1,22fl0/r =
1,22*0,8*5,2 10-7 D/0,04 = 1,27 10-5
m
R=1,22fl0/r =
1,22*0,8 *5,2 10-7 / 5 10-3 =
10-4 m.
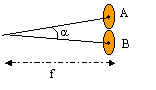
AB = 2R' = af
a=2*1,27 10-5 /0,8
= 3,17 10-5 rad.
a=2*10-4 /0,8 = 2,5
10-4 rad.
un objectif de grande taille donne une plus grande
résolution.
|
|
France Inter : grandes
ondes
Les ondes hertziennes utilisées pour les
émissions de radio et de télévision
sont des ondes électromagnétiques comme les
ondes lumineuses. Leur célérité dans le
vide est c=3.108 m.s-1 ; seules leurs
fréquences diffèrent. On considère une
vallée encaissée rectiligne, d'axe
D. Une onde hertzienne radia
arrive à l'entrée de la vallée. Sa
direction de propagation fait un angle a
avec l'axe D.
- Faire un schéma et montrer que tous les
habitants de la vallée ne pourront pas
écouter cette radio. On appliquera le principe de
propagation rectiligne à cette onde radio.
- On constate que si les habitants ne peuvent pas
capter les ondes de modification de fréquence,
dont la fréquence est de l'ordre de 100 MHz, ils
peuvent, en revanche, capter les " grandes ondes " dont
la fréquence est de l'ordre de 100 KHz.
- Calculer la longueur d'onde des ondes radio de
fréquence 100 MHz et 162 KHz.
- On considère que l'entrée de la
vallée peut être modélisée par
une fente de largeur de l'ordre de kilomètre.
Expliquer pourquoi il est prévu d'utiliser la
radio France Inter Grandes Ondes pour prévenir
tous les français, en cas de crise grave (la
fréquence radio de cette station = 162 KHz.).
corrigé
seules les personnes situées dans la direction
de propagation de l'onde peuvent capter la radio.
f= 108 Hz ; l= 3
108/108 = 3 m.
f= 1,62 105 Hz ; l=
3 108/1,62 105 = 1,851 km.
si l'entrée de la vallée a une largeur de
1km ( ordre de grandeur de la longueur d'onde de
l'émission à 162 kHz), les ondes radio sont
diffractées et toutes les personnes peuvent capter
les émissions.
|
|
diffraction de la
lumière :
- Un rayon laser, de longueur d'onde dans le vide
l, traverse une fente
rectiligne de largeur calibrée notée a. Les
figures de diffraction sont observées sur un
écran placé perpendiculairement au rayon et
à une distance D=4,50 m des fentes ; a est
variable.
- Tracer un schéma donnant l'aspect des figures de
diffraction observées.
- Avec une règle millimétrique est sur la
figure de diffraction, on mesure la distance 2d
séparent les deux premières extinctions
situées de part et d'autre de la tache centrale.
On consigne les résultats dans le tableau suivant
:
|
a(mm)
|
0,3
|
0,2
|
0,1
|
0,05
|
0,025
|
|
2d (mm)
|
13
|
19
|
37
|
73
|
156
|
|
l(µm)
|
|
|
|
|
|
- Justifier l'importance de la dimension de l'obstacle
sur le phénomène de diffraction
observé.
- Donner la relation reliant les grandeurs D,
l, a et d utilisée dans
les expressions précédentes et
préciser la signification et l'unité du
système international de chaque terme.
- Compléter le tableau.
- Quelle est la valeur moyenne de la longueur d'onde de
la radiation émise par l'émetteur laser
?
- Quelle est la couleur correspondant à cette
radiation ?
- Calculer la fréquence de la radiation.
- diffraction par une
fente :
Lors d'une expérience de diffraction, on
relève l'intensité d'une onde lumineuse
diffractée par différentes fentes
rectangulaires de largeur a1 = 0,2 mm,
a2 = 0,5 mm et a3=1 mm. Les courbes
présentant l'évolution de
l'intensité en fonction de l'angle sont
données dans la figure ci-dessous (les
échelles ne sont respectées). La longueur
d'onde dans le vide de la radiation monochromatique
utilisée est égale à 633 nm, et la
célérité des ondes lumineuses dans
l'air est c= 3,00 108 m/s. q
est la demi-largeur de la tache centrale.
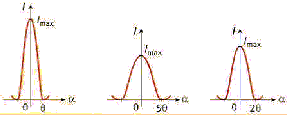
- Quelle est la fréquence de l'onde
diffractée par les fentes ?
- Quelle courbe correspondant à la fente n°1
? à la fente n° 2 ? à la fente n°
3 ?
- Quelle est la largeur de la tache centrale de
diffraction obtenue sur un écran situé
à la distance D=2,5 m de la fente 1
- Une source de lumière blanche éclaire
une fente de largeur a=0,4mm. On observe des taches de
diffraction sur un écran E situé à
2,5 m de la fente.
-R appeler les limites des longueurs d'onde dans le vide
de la lumière visible.
- Si la lumière blanche traverse un filtre
optique, seules certaines longueurs d'onde sont
transmises. On envisage ici trois filtres optiques ;
après avoir traversé l'un de ces filtres,
la lumière est supposée monochromatique, de
longueur d'onde dans le vide : l1
= 541 nm pour le filtre 1 , l2
= 433 nm pour le filtre 2 et l3
= 616 nm pour le filtre 3.
* Donner la couleur de ces trois ondes lumineuses.
* Calculer la largeur de la tache centrale de diffraction
sur l'écran E pour chacune de ces longueurs
d'onde.
* Représenter à l'échelle les trois
taches de diffraction l'une sous l'autre , sachant que
leurs centres ont en réalité la même
position O sur l'écran.
* En ne tenant compte que des taches centrales de
diffraction, décrire la figure de diffraction
obtenue avec la lumière blanche. Indiquer la
position des bords de la tache blanche par rappoirt
à O, et la couleur des irisations qui
bordent.
corrigé
la dimension de l'obstacle et la longueur d'onde de
l'onde doivent être du même ordre de grandeur
pour observer le phénomène de diffraction.
2d = 2lD/a
a: largeur de l'obstacle ou de la fente en m ;
l :longueur d'onde en m ; D
distance fente -écran en m; 2d : largeur de la tache
centrale de diffraction en m.
|
a(mm)
|
0,3
|
0,2
|
0,1
|
0,05
|
0,025
|
|
2d (mm)
|
13
|
19
|
37
|
73
|
156
|
|
l(µm)
|
0,433
|
0,422
|
0,411
|
0,405
|
0,433
|
valeur moyenne : 0,421 µ m (violet)
fréquence : 3 108 / 0,421
10-6 = 7,12 1014 Hz.
fréquence : 3 108 / 0,633 10-6
= 4,74 1014 Hz.
si la largeur de la fente diminue alors q
augmente :
fente 1 : courbe centrale ; fente 2 : courbe de droite ;
fente 3 : courbe de gauche.
d = 2lD/a = 2*0,633
10-6 *2,5 / 2 10-4 =
1,58 cm.
lumière blanche :[400 nm ; 800 nm]
l1 = 541 nm vert
jaune , l2 = 433 nm
violet 2 et l3 = 616
nm orangé.
d1 = 2l1D/a
= 2*0,541 10-6 *2,5 / 4 10-4 =
6,76 mm.
d2 = 2l2D/a
= 2*0,433 10-6 *2,5 / 4 10-4 =
5,41 mm.
d3 = 2l3D/a
= 2*0,616 10-6 *2,5 / 4 10-4 =
7,7 mm.
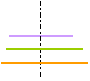
la tache centrale de diffraction ( en lumière
blanche ) est irrisée de rouge orangé.
retour
- menu
|