particule chargée dans un champ électrique cours exercices
dans un champ électrique uniforme le vecteur accélération d'une particule chargée est constant
la déflexion électrique est proportionnelle à la tension appliquée entre les plaques déflectrices
exercice 1 Un faisceau de protons est accéléré... Un faisceau de protons est émis au niveau d'une plaque A, avec une vitesse négligeable. Ces protons sont accélérés entre la plaque A et une plaque C, distantes de 2,5 cm. Les protons atteignent C avec une vitesse de 800 kms-1.La tension appliquée entre les plaques A et C est : 6680 V ; 3340 V ; 6680 Vm-1 ;1,6 kV ; 12540 V. 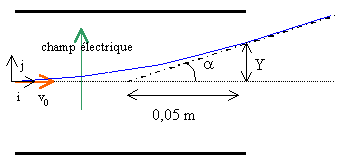masse du proton :1,67 10-27 kg ; e=1,6 10-19 C corrigé L'augmentation d'énergie cinétique est égale au travail de la force électrique remarque : la distance d=0,025 m serait utile pour le calcul de E=U/d 0,5mv2=eU U=0,5mv2 / e avec v=8 105 ms-1 3340 V exercice 2 particule a déviée par un champ électrique Une particule a de masse 6,64 10-27 kg animée d'une vitesse de valeur 1500 kms-1, de direction horizontale, pénètre dans une région de largeur 10 cm, où règne un champ électrique uniforme vertical de 10 000Vm-1. 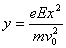En sortant de cette région la trajectoire de la particule fait avec l'horizontale un angle de :......0,0214° ; 0,163° ; 12,3 ° ; 1,23° ; 0,82 ° particule a He2+ charge élémentaire 1,6 10-19C corrigé au départ: accélération ( 0; 2eE/m) vitesse ( V0 ; 0) vecteur position nul à la date t vitesse (V0 ;2eEt/m) position(x=V0t; y=eEt2/m) remplacer x par 0,1 m; v0 par 1,5 106 ms-1 Y=1,07 10-3 m tan a=0.0214 a=1,23° exercice 3 électrons soumis à différents champs électriques 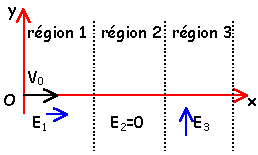E1=2 104 Vm-1 ; e=1,6 10-19 C; m=9 10-31 kg ; V0=2 107 ms-1 ; chaque région a une largeur OA= 4 cm   L'électron atteint-il la région 2 ?; si oui avec quelle vitesse ? Quelle est la durée du parcours de la région 1 ? Quelles sont les composantes des vecteurs vitesse et accélération dans les régions 2 et 3 ? 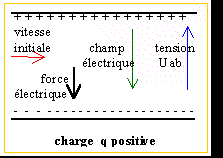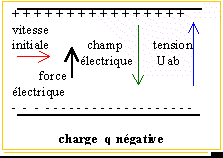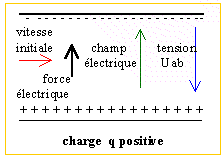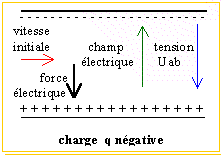corrigé Dans la région 1, la charge négative est soumise à une force électrique colinéaire au champ mais de sens contraire. Les vecteurs vitesse et force étant colinéaires mais de sens contraire, le travail de la force est négatif -eU=-eE1*OA th de l'énergie cinétique DEc=-eU 0,5 mVf² -0,5mV0²= -eE1*OA Vf²=V0² -2e/m *E1*OA La région 2 est atteinte si V0² -2e/m *E1*OA est positive. L'application numérique donne Vf²=1,18 1014 et Vf=1,08 107 ms-1. mouvement rectiligne uniformément retardé (région 1) accélération vitesse position -eE1/m -eE1/m t +V0 -eE1/(2m) t² +V0t -3,51 1015 -1,76 1015t² +2 107 t en A x= 0,04 m il faut résoudre 0,04=-1,76 1015t² +2 107 t t=2,6 10-9 s accélération vitesse nature mouvement région 2 nulle vitesse en A rectiligne uniforme région 3 -e/m E3 abscisse :VA ordonnée -e/m E3temps branche de parabole uniformément accéléré verticale vers le bas oblique vers le bas exercice4 accélération de particules chargées Les particules de vitesse initiale négligeable sont accélérées par une tension U. Dans le cas d'un proton m=1,6 10-27 kg e=1,6 10-19 C, la vitesse finale est 1000 km s-1. Quelle est la valeur de la tension U? La tension garde la valeur précédente, la charge est inchangée mais la masse double; que devient la vitesse ? Dans le cas d'une particule alpha( m asse quadruple et charge double) si U est inchangée que devient la vitesse?. A la place d'un champ électrique peut-on utiliser un champ magnétique pour accélérer ces particules? corrigé 0,5 m v²=eU U=0,5*1,6 10-27*1012 /1,6 10-19 = 5000 V v²=2eU / m Le produit eU gade la même valeur et la masse double : le carré de la vitesse est donc divisé par 2 et la vitesse est divisée par racine carrée de deux Le produit eU double et la masse quadruple : le carré de la vitesse est donc divisé par 2 et la vitesse est divisée par racine carrée de deux La force magnétique perpendiculaire à la vitesse ne travaille pas. l'énergie cinétique donc la valeur de la vitesse sont inchangées. Par contre la direction du vecteur vitesse change. A l'aide de champ magnétique on guide des particules , on ne les accélère pas. th énergie cinétique DEc = q * U joule ..coulomb volt
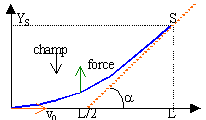
exercice 5 électron dans un champ électrique Un électron de vitesse v0=107 ms-1 traverse une région de longueur L=10 cm où règne un champ électrique E uniforme et perpendiculaire à v0. A la sortie de cette région l'énergie cinétique de l'électron a été multipliée par 3. Calculer et exprimer : l'ordonnée du point de sortie. le travail de la force électrique au cours de ce déplacement. le champ électrique l'angle dont a été dévié l'électron. m = 9,1 10-31 kg ; e = 1 ,6 10-19 C corrigé Le poids de l'électron est négligeable devant la force électrique La trajectoire est une branche de parabole d'équation y= eE x² / (2mv0²) ordonnée du point S d'abscisse L : YS= eEL² /(2mv0²) travail de la force électrique entre le départ et S : e EYS. variation d'énergie cinétique : 3(0,5 mv0²)-0,5 mv0² = mv0² th. de l'énergie cinétique : mv0² = e EYS = eE* eEL² /(2mv0²) E= rac carrée(2) *mv0² /(eL) E=1,414*9,1 10-31 *1014 /(1,6 10-19*0,1)=1414*9,1/1,6= 8042 Vm-1. tan(a)= Ys / (0,5 L)=eEL/mv0² tan(a)= 1,6 10-19*8042*0,1/(9,1 10-31*1014)= 1,6*8,042/9,1 = 1,414 a = 54,7 ° retour - menu