|
BTS batiment (2000) |
|
I hydrostatique- gaz parfaits : 6 points Un local utilisé lors de travaux sous marins est constitué d'un parallélépipède rectangle de hauteur H = 3,0 m et de section horizontale S = 15 m2. Sa partie inférieure est munie d'un orifice lui permettant de communiquer avec l'extérieur. L'air est considéré comme un gaz parfait, sa température garde la même valeur q = 27°C constante dans tous les cas. La pression de l'atmosphère au dessus de l'eau est p0 = 1,0 105 Pa. On rappelle g = 9,81 N. kg-1 ; R = 8,31 SI ; masse volumique de l'eau r = 1,0 10 3 kg.m-3 masse molaire moyenne de l'air: 29 g. mol-1. 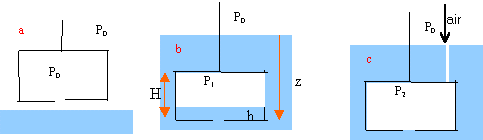
corrigé |
|
PV = nRT P: pression en Pa V volume en m3. n : quantité de matière (mol) T température en kelvin R= 8,31 SI = constante n = PV / (RT) V=3*15 = 45 m3 ; T= 273+27)= 300 K n = 105 *45/(8,31*300) = 1805 mol. schéma b : température, quantité de matière restent inchangés. nouveau volume : 2*15 = 30 m² P1 = 1805*8,31*300 / 30 = 1,5 105 Pa. P1-P0 = r g (z-h) . r masse volumique du liquide z-h (mètre) : différence de niveau entre un point à la surface du liquide dans le caisson et la surface libre du liquide à l'extérieur. z-h = (P1-P0) /( rg) z-h = 0,5 105 / (103*9,8) = 5,1 m d'où z = 5,1+1 = 6,1 m. P2-P0 = r g z . P2 = P0 + rgz P2 = 105 + 103 *9,8*6,1 = 1,597 105 Pa. la quantité de matière d'air a augmenté. n2 = P2V / (RT) n2 = 1,597 105*45/ (8,31*300) = 2884 mol d'air. 2884-1805 = 1079 mol d'air masse d'air : 1079 *29 = 31,29 kg .
|
|
II siphon 7 points 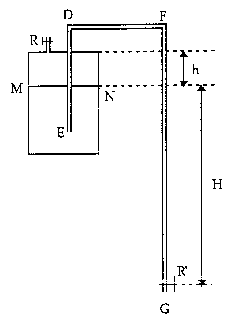 Un vase cylindrique de section S est fermé à sa partie supérieure par un couvercle plan muni d'un robinet R et laissant passer la branche ED d'un siphon EDFG. Ce vase renferme de l'eau dont le niveau MN est à une distance h du couvercle et à une hauteur H au dessus du robinet R' situé à l'extrémité du siphon. Le siphon étant rempli d'eau, le robinet R' étant fermé, on ouvre un instant le robinet R et on le referme. La pression au dessus du liquide est alors égale à la pression atmosphérique, notée patm. On admettra que la section du siphon est négligeable devant celle du vase. On ouvre le robinet R' et on laisse l'eau s'écouler.
corrigé au départ ( R fermé et R' fermé), le volume d'air enprisonné est Sh, sa pression est patm et sa température est T. l'équation des gaz parfait s'écrit : patm Sh = nRT (1) R fermé et R' ouvert, le niveau du liquide dans le vase cylindrique descend de x : le volume de l'air devient alors S(h+x), la pression p, la température ainsi que la quantité de matière d'air n'ont pas changé. l'équation des gaz parfaits s'écrit : p S(h+x) = nRT (2). les deux relations ci dessus donnent : patm Sh = p S(h+x) p = patm h / (h+x). p =
105 *0,1 / (0,1+x) = 104 / (0,1+x).
p + rgz +½rv² = constante. p : pression en pascal r masse volumique du fluide (eau) kg/m3. z altitude en mètre v : vitesse d'écoulement en m/s. On choisi l'altitude du point G comme origine des altitudes. On applique le théorème de Bernoulli entre un point situé à la surface du liquide M et le point G, à la sortie du robinet R'. la vitesse d'écoulement du liquide en M est voisine de zéro si la section du siphon est petite devant la section S du vase. en M : p + r g (H-x) = constante en G : patm + ½ r v² = constante p + r g (H-x) = patm + ½ r v² d'où ½ r v² = p -patm + r g (H-x)= p-105+104(2-x) avec p = 104 / (0,1+x) le liquide ne s'écoule plus lorsque le second membre est nul. ( v =0) : 104 / (0,1+x) -105+104(2-x)=0 réduire au même dénominateur : 104 -105(0,1+x)+ 104(2-x) (0,1+x)=0 effectuer : -105x + 0,2 104 - 104x² +1,9 104x=0 diviser par 104 : -x² -8,1 x +0,2=0 x²+8,1x-0,2 = 0 résoudre : D=8,1²+4*0,2 = 66,41 x1 = (-8,1 +8,149 )/2 = 0,0245 m. la pression de l'air dans le récipient cylindrique fermé est alors : p= 104 / 0,1245 = 80 321 Pa.
retour - menu |